Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 100

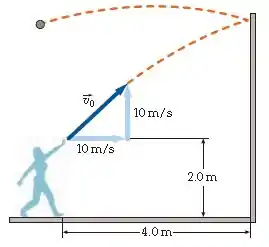
Uma mulher atira uma bola contra um muro vertical 4,0 m à sua frente. A bola está 2,0 m acima do chão quando abandona a mão da mulher com uma velocidade de 14 m/s a 45°, conforme mostrado. Quando a bola atinge o muro, a componente horizontal de sua velocidade é revertida; a componente vertical não se altera. (a) Onde a bola atingiu o chão? (b) Quanto tempo a bola ficou no ar antes de atingir o muro? (c) Onde a bola atingiu o muro? (d) Quanto tempo a bola ficou no ar após abandonar o muro? Ignore a resistência do ar.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

A imagem a seguir pode nos ajudar a entender melhor o enunciado:

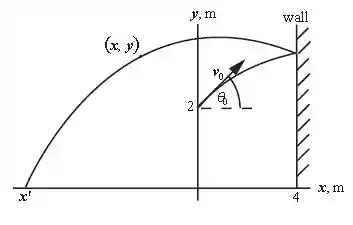
Sabemos que:

x ' = ∆ x - 4   m

Onde x’ é a posição final da bola e ∆ x é seu deslocamento total de ida e volta.

Analisando a posição verticalmente, temos:

y - y 0 = v 0 y t + 1 2 a y t 2

Sabemos que a posição inicial y 0 = h e que a aceleração é a da gravidade para baixo, logo:

y = y 0 + v 0 y t - 1 2 g t 2

y = y 0 + ( v 0 sin ⁡ θ ) t - 1 2 g t 2

∆ y = ( v 0 sin ⁡ θ ) t - 1 2 g t 2

Substituindo os valores, temos:

- 2 = ( 14 sin ⁡ 45 ° ) t - 1 2 9,81 t 2

Resolvendo a equação, podemos encontrar o tempo de vôo que é:

t = 2,203   s

Vamos fazer uma analise horizontal do movimento agora:

∆ x = v 0 cos ⁡ θ ⋅ t

∆ x = 14 ⋅ cos ⁡ 45 ° ⋅ 2,203

∆ x = 21,8   m

Logo:

x ' = 21,8 - 4

x ' = 17,8   m

A bola cai 17,8 metros atrás da mulher.

Passo 2

Para o tempo de vôo até atingir a parede, temos:

∆ t p a r e d e = ∆ x p a r e d e v 0 c o s θ

Substituindo os valores:

∆ t p a r e d e = 4 14 ⋅ cos ⁡ 45 °

t = 0,4041   s

Passo 3

Agora temos que encontrar o ponto em y onde a bola atingiu o muro. Temos que:

y = 2 + ( 14 ⋅ sin ⁡ 45 ° ) ⋅ 0,4041 - 1 2 ⋅ 9,81 ⋅ 0,4041 2

y = 5,199   m

Passo 4

Para descobrir o tempo de vôo da bola após atingir o muro devemos saber a velocidade inicial do movimento após atingir o muro:

v y = v 0 y - g ∆ t p a r e d e

v y = v 0 sin ⁡ θ - g ∆ t p a r e d e

v y = 14 ⋅ sin ⁡ 45 ° - 9,81 ⋅ 0,4041

v y = 5,935   m / s

Logo:

y f = y 0 ' + v y ⋅ ∆ t p a r e d e ∆ t ' - 1 2 g ∆ t ' 2

0 = 5,199 + 5,935 ⋅ 0,4041 ∆ t ' - 1 2 g ∆ t ' 2

∆ t ' = 1,789   s

Resposta

a ) x ' = 17,8   m

b ) t = 0,4041   s

c ) y = 5,199   m

d ) ∆ t ' = 1,789   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um foguete é lançado verticalmente do repouso, com uma aceleração ascendente constante de 1,75m / s 2 . Após 22,0s do lançamento, um tanque de combustível não mais necessário é desconectado do foguete
Em uma comemoração de 04 de julho (Dia da Independência dos EUA), um rojão é lançado do nível do solo com velocidade inicial de 25,0m / s e ângulo de 30 ° da vertical. Ao atingir sua altura máxima, el
Atirando o almoço. Henriqueta está indo para a aula de física e corre pela calçada a 3,05m / s . De repente, seu marido Bruno percebe que ela saiu com tanta pressa que esqueceu o sanduíche. Ele corre
Um projétil é disparado do ponto A de um ângulo sobre a horizontal. No seu ponto mais alto, após ter percorrido uma distância horizontal D a partir do seu ponto de lançamento, ele explode e se parte e
Você quer treinar para malabarista, mantendo duas bolas no ar, e suspendendo-as até uma altura máxima de 2m.De quanto em quanto tempo e com que velocidade tem de mandar as bolas para cima?