Uma pedra de 0,050 kg se move dá origem ao ponto(3,0 m, 5,0 m) em um sistema de coordenadas no qual o sentido positivo do eixo Oy é de baixo para cima. a) A pedra inicialmente se move horizontalmente dá origem ao ponto(3,0m, 0) e a seguir ela se move verticalmente do ponto (3,0 m, 0) ao ponto (3,0, 5,0 m).Faça um esboço da trajetória da pedra no plano xy. Qual é o trabalho realizado pela força gravitacional durante esse deslocamento?b) Em vez de a trajetória indicada na parte (a), suponha que a pedra inicialmente se move verticalmente dá origem ao ponto (0, 5,0m) e a seguir se move horizontalmente de (0, 5,0 m) ao ponto (3,0, 5,0 m). Faça um esboço da trajetória da pedra no plano xy. Qual o trabalho realizado pela força gravitacional durante esse deslocamento? c) Comparando suas respostas dos itens (a) e (b), você pode dizer se a força gravitacional é conservativa ou não conservativa?Explique
Passo 1
Beleza pessoal?! Espero que esteja tudo bem com meu os herdeiros de Newton. Vamos dar início a mais uma resolução com o padrão de qualidade do Responde aí, então pegue seu lápis, caderno e café e vamos nessa!!!
Nesta tarefa, calculamos o trabalho da gravidade quando a rocha é transferida para o mesmo ponto, mas de maneira diferente. O trabalho é definido como o produto escalar da força pelo vetor deslocamento.
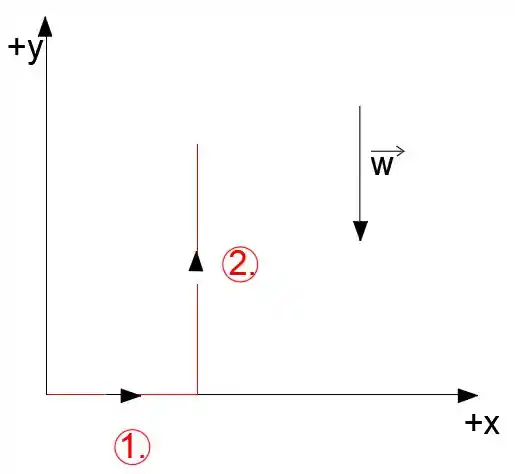
a) Na figura abaixo podemos ver o movimento da rocha, primeiro ela se move ao longo do eixo x em 3 m e depois se move ao longo do eixo y em 5m. O trabalho total realizado na rocha é igual à soma dos trabalhos
O trabalho total para a rota 1 é:
Passo 2
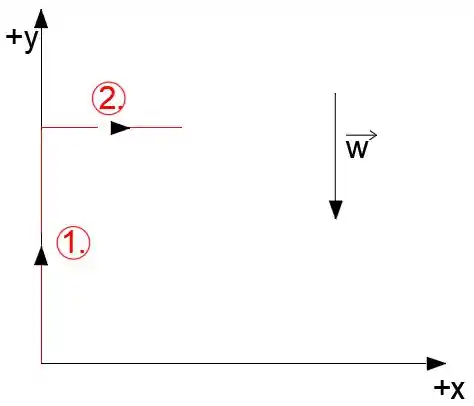
b) Na figura abaixo podemos ver o movimento da rocha, primeiro ela se move ao longo do eixo y em 5m e depois se move ao longo do eixo x em 3m. O trabalho total realizado sobre a rocha é igual à soma dos trabalhos
O trabalho total para a rota 2 é:
Passo 3
c) O trabalho total dos dois caminhos diferentes é igual:
d) A força gravitacional é uma força conservativa porque o trabalho feito para caminhos diferentes, mas o mesmo ponto final, é o mesmo.
Resposta
- -2.45 J
- -2.45 J