Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 7.1 - Ex. 13
Um forno de microondas de 10,0 kg é empurrado 6,0 m para cima de uma rampa inclinada de um ângulo de 36,9° acima da horizontal, por uma força constante de módulo igual a 110 N atuando paralelamente ao deslocamento ao longo da rampa. O coeficiente de atrito cinético entre o forno e a rampa é igual a 0,250.
a) Qual é o trabalho realizado pela força sobre o forno?
b) Qual é o trabalho realizado sobre o forno pela força de atrito?
c) Calcule o aumento da energia potencial para o forno.
d) Use suas respostas das partes (a), (b) e (c) para calcular o aumento da energia cinética do forno.
e) Use para calcular a aceleração do forno. Supondo que o forno esteja inicialmente em repouso, use a aceleração do forno para calcular sua velocidade depois de se deslocar 8,0 m. A partir daí calcule o aumento de energia cinética e compare o resultado com o obtido no item (d).
Passo 1
Abaixo temos a figura esquematizando o problema,
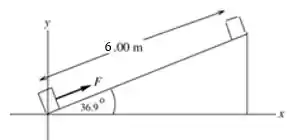
é constante, então, para encontrarmos o trabalho, usaremos a seguinte equação
Podemos encontrar a , na origem; transportando o eixo y para a direita relacionamos com o seno
Assim,
Passo 2
Para achar o trabalho da força de atrito, precisaremos destrinchar o sistema e achar as forças
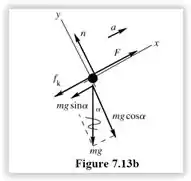
Fazendo ,
Como , então
Então o trabalho dessa força é de
negativo, porque a força de atrito é contrária ao movimento.
Passo 3
Para o aumento da energia potencial, y = 0 na parte inferior da rampa, pois o forno parte do repouso (origem)
Enquanto para o aumento de energia cinética, vamos fazer por
Sendo ,
Logo,
Passo 4
A letra “e” nos pede a aceleração do forno e o aumento de energia a partir disso, então vamos lá!
Assim, isolando “a”
Para acharmos a velocidade, vamos utilizar uma das equações de movimento
O aumento de energia cinética é
Resposta
a)
b)
c)
d)
e); .