Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 7.Problemas - Ex. 3

Um fóton de 100   M e V colide com um próton em repouso. Calcule a perda máxima de energia que o fóton pode sofrer

Passo 1

Vamos entendero que está acontecendo:

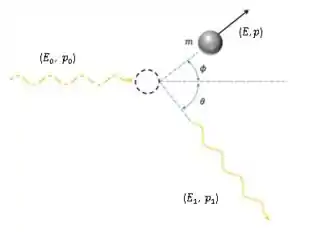
O fóton colide com um proton em repouso, que adquire uma energia cinética.

A energia perdida pelo fóton é absorvida pelo próton na forma de energia cinética, k . Pela conservação de energia total relativística;

E i = E f

E 0 + m e c 2 = E 1 + E

E 0 + m e c 2 = E 1 + k + m e c 2

Onde m e c 2   é a energia de repouso do próton.

Como

E = h f = h c λ

Temos

h c λ 0 + m e c 2 = h c λ 1 + k + m e c 2

h c λ 0 = h c λ 1 + k

Então a energia cinética do próton é:

k = h c λ 0 - h c λ 1

Beleza! Vamos por partes.

O fóton incidentente tem energia 100 M e V . Ou seja:

E 0 = 100 M e V = 100   10 6   1,6   10 - 19 J = 1,6 × 10 - 11 J

Sabemos que

E 0 = h f 0 = h c λ 0

λ 0 = h c E 0

λ 0 = 6,626 × 10 - 34 3 × 10 8 1,6 × 10 - 11

λ 0 = 1,24 × 10 - 14 m

Beleza! Sabemos o comprimento de onda do fóton incidente.

Vamos descobrir o comprimento de onda do fóton depois da colisão.

O deslocamento Compton é dado por:

Δ λ = λ 1 - λ 0 = h m e c 2 1 - cos ⁡ θ

Agora,pensa junto aqui comigo: Se θ = 0 , Δ λ = 0 , temos uma colisão de raspão,o fóton incidente mal é desviado. Agora, se θ = 18 0 ° , Δ λ = 2 h m e c 2 , temos uma colisão onde o fóton incidente tem o sentido invertido. É uma colisão frontal, o fóton acerta o próton com tudo! Então é esse valor de θ que nos dará uma maior energia cinética para o próton.

Δ λ = λ 1 - λ 0 = 2 h m e c 2

λ 1 = 2 h m e c 2 + λ 0

λ 1 = 2 ( 6,626 × 10 - 34 ) 1,67 × 10 - 27 3 × 10 8 2 + 1,24 × 10 - 14

λ 1 = 1,5 × 10 - 14 m

Então, a perda máxima de energia do fóton, que igual a energia cinética máxima adquirida pelo próton é:

k = h c λ 0 - h c λ 1

k = ( 6,626 × 10 - 34 ) ( 3 × 10 8 ) 1,24 × 10 - 14 - ( 6,626 × 10 - 34 ) ( 3 × 10 8 ) 1,5 × 10 - 14

k = 2,81 × 10 - 12 J

Passando para M e V :

k = 2,81 × 10 - 12 1,6 × 10 - 19

k = 17,6 M e V

Resposta

k = 17,6 M e V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para verificar se o conceito de fóton é relevante no eletromagnetismo microscópico, considere uma estação de rádio que transmite na frequência de 1M H z e com uma potência total emitida de 5k W . (a)
38.50. Supergigantes azuis. Uma típica estrela supergigante azul (o tipo que explode deixando buracos negros para trás) apresenta uma temperatura de superfície próxima a 30000 K e uma luminosidade vis
Mostre que o máximo na distribuição de Planck, Equação (38.32), ocorre para um comprimento de onda λ m dado por λ m = h c 4,965k T , equação (38.33). Conforme discutido no texto, 4,965 é a raiz da equ
Considere o seguinte vetor de estado de polarização de um fóton: Ψ = 1 + i 2 + + 1 - i 2 - onde + e – são os vetores de estado normalizados de polarização circular esquerda e direita, respectivamente.
Mostre que, na representação em que θ = 1 2 e - i θ e i θ o observável P ^ θ (polarização linear do fóton na direção θ ) é representada pela matriz P ^ θ = 1 2 1 e - 2 i θ e 2 i θ 1