O freio de um caminhão de massa m deixa de funcionar quando ele está descendo uma estrada de montanha com gelo inclinada de um ângulo (Figura 7.40). Inicialmente o caminhão desce a montanha com velocidade . Depois de percorrer com atrito desprezível uma distância até a base da montanha, o motorista vira o volante e faz o caminhão subir uma rampa de emergência para caminhões inclinada para cima com um ângulo constante. A rampa para caminhões é pavimentada com areia fofa que possui um atrito de rolamento igual a . Qual é a distância percorrida pelo caminhão ao subir a rampa até parar? Use o método da energia.

Vamos aplicar a equação da conservação da energia:

energia cinética

energia potencial

para as posições inicial e final do caminhão.

Deixe no ponto mais baixo do caminho do caminhão.

é o trabalho feito por atrito.

A força de atrito é dada por:

o ângulo entre a reta normal e a componente do peso que age no caminhão e contribui para a força de atrito

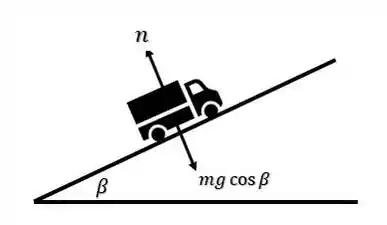
Indicando a distância que o caminhão move a rampa por , temos que:

E

Para:

e resolvendo para :

Dividindo todo mundo por :

aumenta quando aumenta e diminui quando aumenta.