Um gás ideal, inicialmente a 20°C e a 200 kPa, tem um volume de 4,0L. Ele sofre uma expansão isotérmica quase estática até que sua pressão seja reduzida para 100 kPa. Determine:

1. O trabalho realizado pelo gás;
2. O calor absorvido pelo gás durante a expansão.

Bom, na letra a queremos achar o trabalho realizado pelo gás. É bem importante lembramos aqui que o trabalho pode ser obtido através da área abaixo de um gráfico PV, formado pela trajetória do gás indo de 1 até 2.

Sabemos que o gás se expande de até , que não foi fornecido, com a consequente redução da pressão de até à temperatura constante.

Talvez essa informação pode passar batida por vocês, mas ela vai influenciar no formato do nosso caminho e na área abaixo do gráfico, ok?

Desenhando o diagrama:

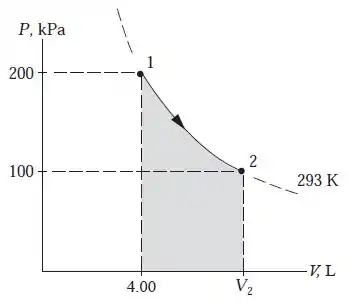
Como a área abaixo desse gráfico é o trabalho, temos:

Para o gás nós podemos lembrar da seguinte relação:

Isolando P:

Substituindo na integral:

Resolvendo a integral:

Para o primeiro passo:

Chegamos em um empasse! Não sabemos nRT, mas sabemos que é uma constante e pela relação mostrada anteriormente:

Agora sim! Pressão e volume nós temos, mas qual usar? Do ponto 1 ou 2?

Não importa! Isso mesmo, você pode estar achando estranho, mas o fato de sua multiplicação produzir uma constante válida para os dois pontos podemos escolher qualquer um, mas vou optar pelo ponto 1 já que não sabemos o volume final:

Agora já conseguimos calcular o trabalho? A resposta é não! Não sabemos qual é o volume final, então vamos relacioná-lo com algo que sabemos:

No trabalho:

Agora sim, sabemos todas as variáveis. Bora substituir?

Mas calma, nosso volume está em litros, então vamos transformá-lo em m³:

Finalizamos a letra a e agora podemos passar para b.