Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.6 - Ex. 53
O gráfico na Figura 2.43 descreve a aceleração em função do tempo para uma pedra que rola colina abaixo, a partir de uma posição de repouso. a) Determine a variação na velocidade da pedra, entre e . b) Faça um gráfico da velocidade da pedra em função do tempo.
Passo 1
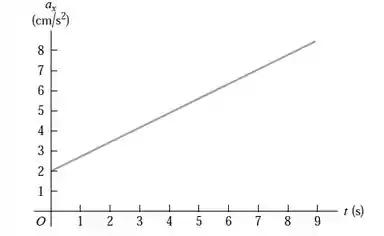
Opa, bora resolver esse problema! O enunciado nos dá o seguinte gráfico da aceleração de uma pedra rolando de um morro:
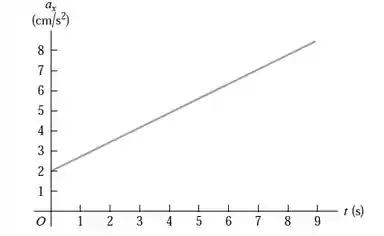
A primeira coisa que devemos fazer é calcular a variação na velocidade da pedra, entre e .
A variação de velocidade que queremos é a integral da aceleração no intervalo de tempo dado e a integral é nada mais nada menos do que a área sobre a curva!
Sabemos que a área é dada por:
Pelo gráfico, temos que:
Passo 2
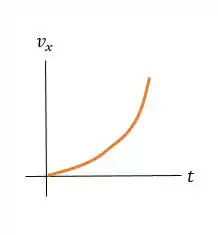
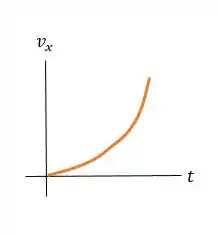
Agora a gente tem que fazer um gráfico da velocidade da pedra em função do tempo!
A inclinação no gráfico é positiva e está aumentando com o tempo, :
Resposta
a)
b) 