Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.Problemas - Ex. 77
Uma partícula se move em um plano . Suas coordenadas são dadas em função do tempo por
onde e são constantes.
a) Faça um esboço da trajetória da partícula. (Essa curva é a trajetória de um ponto que se desloca na periferia de uma roda que rola com velocidade escalar constante numa superfície horizontal. A curva traçada por esse ponto enquanto ele se move no espaço denomina-se ciclóide.)
b) Determine os componentes da velocidade e da aceleração da partícula em qualquer tempo t.
c) Para que instantes a partícula está momentaneamente em repouso? Quais são as coordenadas da partícula nesses instantes? Determine o vetor aceleração.
d) O módulo da aceleração é função do tempo? Compare com o movimento circular uniforme.
Passo 1
E aí! tudo certinho!
Nesse problema temos uma partícula se move em um plano . Suas coordenadas são dadas em função do tempo por
onde e são constantes.
A partir dessas equações temos que obter algumas coisas...
Temos que fazer um esboço da trajetória da partícula, determinar os componentes da velocidade e da aceleração da partícula em qualquer tempo t, obter os instantes a partícula está momentaneamente em repouso e as coordenadas da partícula nesses instantes.
Além disso queremos determinar o vetor aceleração e responder se o módulo da aceleração é função do tempo.
Muita coisa, não é?
Vamos por partes...
Passo 2
Essa trajetória é periódica, então precisamos determinar alguns pontos.
Sabemos que as funções seno e cosseno tem seus valores entre , no entanto, quando um é máximo/mínimo, o outro é zero.
Em :
Em :
Em :
Em :
Juntando todas essas informações e com a ajuda de um gerador gráfico podemos esboçar o gráfico :
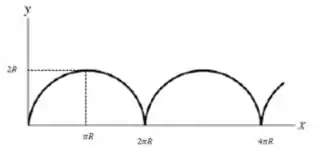
Show?
Passo 3
A velocidade é a derivada temporal da posição. Como temos as expressões para as posições e , é só derivar essas duas e encontrar e respectivamente.
Tranquilo até aqui?
Passo 4
E a aceleração é a derivada temporal da velocidade. No passo anterior calculamos as componentes da velocidade, e a partir delas podemos calcular as componentes da aceleração.
Bacana, não é?
Passo 5
A partícula está momentaneamente em repouso quando sua velocidade é zero:
Das equações temos:
Ou
Ou seja, quando for:
Ou seja, nas posições:
E o vetor aceleração no primeiro instante que isso acontece, ou seja, em é:
Vertical para cima:
Estamos quase lá!
Passo 6
O módulo da aceleração vai ser dado pela raiz da soma do quadrado das componentes:
Como na letra calculamos as componentes (passo ) vamos resgatar de lá a expressão para e e substituir ali em cima no módulo de :
E lembrando da relação trigonométrica fundamental , então temos o módulo da aceleração:
Que é a mesma aceleração do movimento circular uniforme e independe do tempo.
E fim! Entendeu tudo? Responde Aí!
