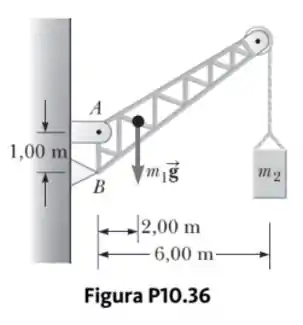
Um guindaste de massa suporta uma carga de massa , conforme mostrado na Figura P10.36. O guindaste é articulado com um pino sem atrito em e se apoia em um suporte liso em . Encontre as forças de reação no

1. ponto e
2. no ponto .

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Nós interpretamos o problema para o suporte no ponto B ser sem atrito. Então o suporte exerce uma força na direção x e:

E

Essas equações se combinam para dar as magnitudes dos componentes:

As forças são:

E