Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 10.Problemas - Ex. 43

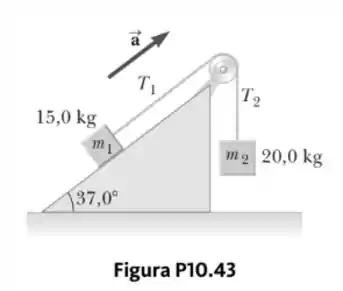
Como mostrado na Figura P10.43, dois blocos são conectados por uma corda de massa desprezível passando sobre uma roldana de raio r   =   0,250   m e momento de inércia I . O bloco na rampa sem atrito move-se com aceleração constante de módulo a   =   2,00   m / s 2 . A partir dessas informações, queremos encontrar o momento de inércia da roldana.

  1. Que modelo de análise é apropriado para os blocos?
  2. Que modelo de análise é apropriado para a roldana?
  3. A partir do modelo de análise na parte (a), encontre a tensão T 1 .
  4. Do mesmo modo, encontre a tensão T 2 .
  5. A partir do modelo de análise na parte (b), encontre uma expressão simbólica para o momento de inércia da roldana quanto às tensões T 1 e T 2 , o raio da r da roldana e a aceleração a .
  6. Encontre o valor numérico do momento de inércia da roldana.

Passo 1

E aiii gente, tudo bem com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo!

Letra a:

Vamos aplicar a segunda lei de Newton à massa m 1 :

T 1 - m 1 g s i n ⁡ 37.0 ∘ = m 1 a T 1 = ( 15.0 k g ) 9.80 sin ⁡ 37.0 ∘ + 2.00 m / s 2 = 118 N

E à massa m 2 :

m 2 g - T 2 = m 2 a T 2 = m 2 ( g - a ) = 20.0 k g 9.80 m s 2 - 2.00 m s 2 = 156 N

Passo 2

Letra b:

T 2 - T 1 R = I α = I a R

I = T 2 - T 1 R 2 a = ( 156 N - 118 N ) ( 0.250 m ) 2 2.00 m s 2 = 1.17 k g ⋅ m 2

Resposta

  1. 118 N   e   156 N
  2. 1.17 k g ⋅ m 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma forma de identificar se um ovo está cozido ou não sem quebrá-lo, é colocar o ovo sobre uma superfície horizontal rígida e tentar girá-lo. Um ovo cozido vai girar com facilidade, contrariamente ao
Verdadeiro ou falso: Se o torque resultante sobre um objeto em rotação é zero, a velocidade angular do objeto não pode mudar. Se sua resposta é “falso”, dê um exemplo de tal situação.
Um bloco deslizando sobre uma mesa sem atrito está amarrado a um fio que passa por um pequeno furo através da mesa. Inicialmente, o bloco está deslizando com rapidez v 0 em um círculo de raio r 0 . Um
Você está andando em direção ao norte, e na sua mão esquerda você está carregando uma mala que contém uma roda massiva girante, montada sobre um eixo preso às partes anterior e posterior da maleta. A
Na figura, o plano inclinado é sem atrito e o fio passa pelo centro de massa de cada bloco. A polia tem um momento de inércia I e raio R . (a) Determine o torque resultante sobre o sistema (as duas ma