Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 94
. Uma haste de e de comprimento está suspensa verticalmente por um eixo horizontal, livre de atrito, que passa por seu centro. Uma bola de argila de , deslocando-se horizontalmente a , colide com a haste e gruda-se exatamente à sua extremidade inferior. Até que máximo valor de ângulo, medido com relação à vertical, a haste (junto com a argila) irá girar?
Passo 1
Um esquema é:
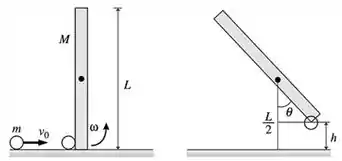
Nós já temos:
Nós estamos atrás de
Passo 2
Sabemos que :
Também sabemos que
Como
Se é a velocidade final da bola e a bola gruda na haste,
Passo 3
Aplicando conservação do momento angular, com nossas deduções do :
Nós já temos:
Passo 4
Aplicando conservação da energia
Nós já temos:
Resposta
Exercícios de Livros Relacionados
Um cilindro de massa M e raio R possui uma densidade cresce linearmente a partir do seu eixo, p = ar, onde aé uma constante positiva, a) Calcule o momento de inércia do cilindro relação a um eixo long
Exatamente uma volta de uma corda flexível de massa m é enrolada na periferia de um cilindro uniforme maciço de massa M e raio R . O cilindro gira sem atrito em tomo de um eixo horizontal ao longo do
Uma hélice de avião possui massa de 117 kg e comprimento igual a 2.08m (de uma extremidade a outra). A hélice está girando a 2400 rev/min em relação a um eixo que passa pelo seu centro.Qual é a sua en
Desejamos armazenar energia em um volante de 70.0kg que possui forma de um disco maciço uniforme com raio R = 1.20m. Para impedir danos estruturais, a aceleração radial máxima de um ponto na sua perif
Taxa de perda da energia cinética. Um corpo rígido com momento de inércia I gira uma vez a cada T segundos. A velocidade de rotação está diminuindo, de modo que dT/dt0.Expresse a energia cinética da r