Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 65
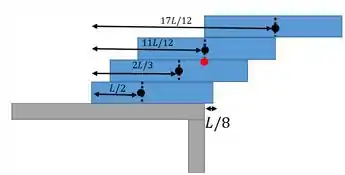
|| Sua tarefa em um concurso de ciência é empilhar quatro blocos idênticos, cada um de comprimento , até que o tijolo superior fique o mais à direita possível sem que a pilha desabe. É possível, como mostrado na , empilhar os tijolos de modo que nenhuma parte do tijolo superior esteja sobre a mesa? Responda a esta questão determinando o máximo valor possível para .
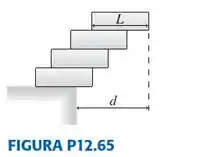
Passo 1
Para resolver vamos usar e fórmula do centro de massa dois a dois, começando pelo bloco de baixo até o último.
Centro de massa:
Lembrando que as massas serão iguais.
O centro de massa sempre será essa última parte da direita, mas não necessariamente a metade.
No primeiro empilhamento, o bloco 1 pode se estender do 2 no máximo em :
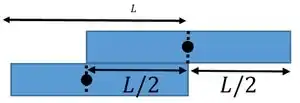
Passo 2
Pós combinação do bloco 1 e 2:
Então o bloco 2 pode se estender do 3 em :
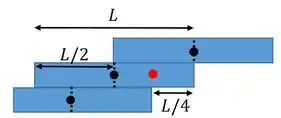
Passo 3
Pós combinação dos blocos 1 ,2 e 3 :
Então o bloco 3 pode se estender do 4 em :
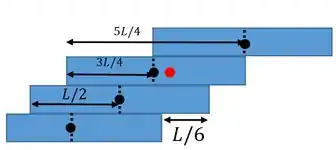
Passo 4
Pós combinação dos blocos 1 ,2 , 3 e 4:
Então o bloco 4 pode se estender da mesa em :
Passo 5
Calculamos a extensão total:
Como , então:
Sim é possível empilhar os tijolos de modo que nenhuma parte do tijolo superior esteja sobre a mesa.
Resposta
Sim é possível empilhar os tijolos de modo que nenhuma parte do tijolo superior esteja sobre a mesa.