Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 74
Um helicóptero de está baixando um caminhão de até o chão por um cabo de comprimento fixo. O caminhão, o helicóptero e o cabo estão descendo a e devem ser freados até nos seguintes de descida para evitar danos ao caminhão. Suponha constante a taxa de freamento. (a) Desenhe o diagrama de corpo livre do caminhão. (b) Determine a tensão do cabo. (c) Determine a força de sustentação sobre as pás do helicóptero.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O diagrama de corpo livre, para a situação descrita, está exposto abaixo:
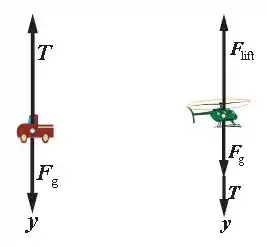
Passo 2
Aplicando a segunda lei de Newton no caminhão, temos:
Temos que:
Agora que encontramos a aceleração, podemos aplicar na nossa equação para encontrar a tensão:
Passo 3
Para o helicóptero, temos:
Resposta
Exercícios de Livros Relacionados
Uma corrente é constituída de 5e l o s , cada um de massa 0,1k g . A corrente está sendo puxada para cima por uma força aplicada por sua mão no elo superior, dando à corrente uma aceleração para cima
Um bloco de 2,0k g está pendurado em uma escala de mola calibrada em newtons que está pressa no teto de um elevador (Figura 4-49). Qual a leitura da escala quando (a) o elevador está subindo com uma r
Dois objetos estão ligados por um fio sem massa, como mostrado na Figura 4-54. O plano inclinado e a polia sem massa não têm atrito. Encontre a aceleração dos objetos e a tensão no fio (a) em termos d
Uma caixa de massa m 2 = 3,5k g está sobre uma estante horizontal sem atrito e presas por fios a caixas de massas m 1 = 1,5k g e m 3 = 2,5k g , como mostra a Figura 4-51. As duas polias são sem atrito
Durante uma apresentação teatral de Peter Pan, a atriz de 50k g que representa Peter Pan deve voar verticalmente (descendo). Para acompanhar a música ela deve, a partir do repouso, ser baixada de uma