Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 2.1 - Ex. 84
Dois trens viajam em sentidos opostos, em trilhos paralelos. Eles estão inicialmente em repouso e suas frentes estão distantes 40 m. O trem à esquerda acelera para a direita a 1,0 m/s². O trem à direita acelera para a esquerda a 1,3 m/s². (a) Qual a distância percorrida pelo trem da esquerda até que as frentes dos trens se cruzem? (b) Se cada trem tem um comprimento de 150 m, quanto tempo após a largada eles terão completamente ultrapassado um ao outro, supondo constantes suas acelerações?
Passo 1
a) Oi pessoal, tudo bem? Vamos analisar essa questão. Temos dois trens saindo do repouso com as acelerações e posições da figura:
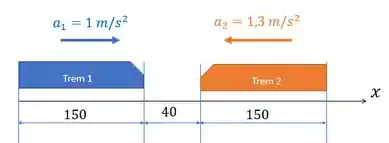
Primeiro, vamos separar os trens e chamar de 1 o da esquerda e 2 o da direita.
Ele quer saber a distância percorrida pelo trem 1 até que as frentes dos dois trens se encontrem. Uma forma de resolver essa é achar o instante em que esse dois trens se encontram e depois descobrir a posição do trem 1 nesse instante em relação a sua posição inicial.
Como temos aceleração constante nos dois casos, podemos usar as expressões de aceleração constante. Por exemplo, podemos usar a equação da posição:
Onde é a posição inicial, é a velocidade inicial e é a aceleração. Vamos começar escrevendo a equação da posição da frente do trem para o trem 1 e para o trem 2.
Passo 2
Nosso referencial de origem vai ser a frente do trem 1. Logo a posição inicial dele é nula. Como ele sai do repouso, a velocidade inicial dele também é nula, então para expressar a posição do trem 1, temos:
Em relação a frente do trem 1, a posição da frente do trem 2 está em . A velocidade inicial dele também é nula. Logo, a posição do trem 2 é dada por:
As frentes dos trens se cruzarão quando suas posições forem as mesmas:
Substituindo as expressões que a gente montou:
Isolando, conseguimos achar o instante onde há o encontro:
Passo 3
Lembra que a gente quer a posição do trem 1 quando há esse encontro? Então vamos substituir esse na equação da posição do trem 1:
A posição do trem 1 será então:
Substituindo os dados do problema:
Passo 4
b) Queremos o tempo que leva para que os trens tenham se ultrapassado completamente. Como é o tempo em relação a largada, a gente só precisa achar o instante em que eles se encontram.
Vamos refletir. No item anterior a gente estudou a posição das frentes dos trens. Agora a gente vai estudar a posição das suas partes de trás.
Por que? Cara, se as partes traseiras dos trens estiverem na mesma posição, significa que um trem passou completamente pelo outro, certinho?
Então vamos montar a equação da posição para as partes traseiras dos trens. Uma dica: o que vai ser bem importante é como o nosso referencial de posição vai mudar, beleza? Lembrando que a equação para aceleração constante é:
E que ambos os trens tem de comprimento como na nossa figura:
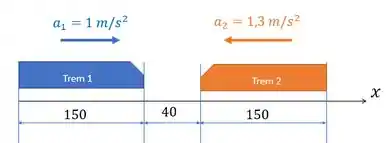
Os dois trens saem do repouso. Então para os dois temos . Aí vamos montar a equação da posição para a traseira do nosso trem da esquerda. Vamos colocar a origem do nosso referencial na traseira do trem 1. Assim para ele :
Já a traseira do trem 2 vai começar inicialmente a uma distância da nossa origem de
De modo que sua posição é
Queremos o instante onde essas partes de trás dos trens estão na mesma posição, então fazemos :
Isolando o instante que queremos encontrar:
Substituindo os dados: