Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 3.Exercícios e Problemas - Ex. 1
Indo para o trabalho, João caminha na direção leste (direção ), segue depois para o sul (direção ) e caminha . Chega ao edifício onde trabalha, toma o elevador e sobre (direção ). Calcule: A) o módulo do deslocamento de João; B) o ângulo entre e a direção norte.
Passo 1
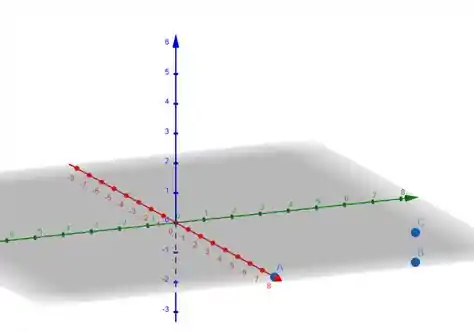
Salve pessoas, tudo certo? Então, nesta questão iremos abordar como os vetores funcionam no tocante a módulo e ângulo entre vetores, okay? Primeiro vamos adotar a casa de João como a origem da coisa toda. Daí ele caminha na direção , e a questão ainda nos diz que é a direção leste. Só por ai já sabemos que: Direção norte se dá por , direção sul se dá por e direção oeste se dá por Continuando, ele depois segue para o sul por e depois sobe na direção . Representei isso graficamente na imagem abaixo:
Passo 2
Para acharmos o item (A), é bem simples. O módulo desse vetor é dado por:
Passo 3
Para o item (B), o ângulo entre o vetor do módulo e a direção norte (). Usaremos a formula de:
Onde é igual ao seno do ângulo do plano formado entre os vetores com seu produto vetorial (que é ), ou seja: . Já o e é o módulo de cada vetor, portanto:
Isolando :