Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.Problemas Adicionais - Ex. 133
Um pacote de , inicialmente em repouso, explode em três partes que deslizam em um piso sem atrito. O pacote estava inicialmente na origem de um sistema de coordenadas. A parte tem massa e velocidade . A parte tem massa , uma velocidade escalar de e sua trajetória faz um ângulo de (no sentido anti-horário em relação ao semi-eixo positivo). (a) Qual é a velocidade escalar da parte 3? (b) Em que direção ela se move?
Passo 1
Vamos começar escrevendo a velocidade da parte em termos dos vetores unitários.
Beleza, com isso já podemos fazer uma expressão para o momento linear total do sistem após a explosão:
Já que o sistema estava inicialmente em repouso, pela lei de conservação do momento linear, essa soma tem que ser igual a zero durante todo o tempo. Então:
Passo 2
Agora vamos resolver essa expressão para encontrar :
E já que a massa total do pacote é :
Então:
Passo 3
(a) Agora podemos calcular o módulo desse vetor:
(b) E para definir a sua direção só precisamos calcular o seu ângulo em relação ao semi-eixo positivo de .
Mas como as duas componentes do vetor são negativas, isso quer dizer que estamos no teceiro quadrante do plano:
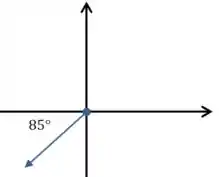
Então o ângulo em relação ao semieixo positivo em é:
Resposta
(a) O módulo da velocidade é .
(b) O vetor forma um ângulo de com o semieixo positivo no sentido anti-horário.