Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 12.Problemas - Ex. 16
Um ioiô de massa , raio interno , raio externo e momento de inércia em relação ao seu centro e massa, é puxado pelo fio enrolado em seu eixo central, de forma a rolar sem deslizamento sobre uma mesa horizontal, através de uma força que faz um ângulo com a horizontal (Fig)
Passo 1
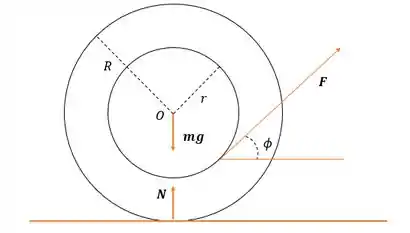
(a) Para que o ioiô permaneca em cotato com a mesa, a normal deve ser não nula. No eixo , teremos o seguinte:
Para nossa situação , assim:
Então,
(b) Como queremos saber a aceleração angular , podemos calcular o analisar o torque com relação ao centro do ioiô.
Assim,
Nessa situaçã
No eixo :
Passo 2
Agora vamos juntar as coisas.
Usando na terceira equação que :
Subsbtituindo na primeira equação:
Isolando o :
Assim,
Passo 3
No caso do ângulo critico ocorre para , logo:
Isto é,
O carretel irá rodar no sentido anti-horário
O carretel irá rodar no sentido horário