Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 11.4 - Ex. 14
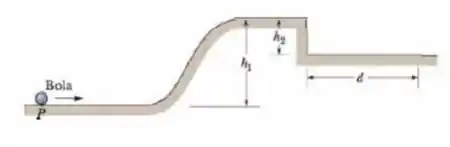
Na figura abaixo uma bola pequena, homogênea é lançada do ponto P, rola suavemente em uma superfície horizontal, sobe uma rampa e chega a um platô. Em seguida, deixa o platô horizontalmente para pousar em outra superfície mais abaixo, a uma distância horizontal da extremidade do platô. As alturas verticais são e . Com que velocidade a bola deve ser lançada do ponto P para pousar em ?
Passo 1
Olá, tudo bem? Vamos começar?
Pelo princípio da conservação da energia temos que a energia cinética (rotação mais translação) no ponto vai ser igual a energia total no platô. E no platô temos a energia cinética de rotação, a energia cinética de translação e a energia potencial. Como a bola rola sem deslizar, a relação é válida aqui. Sendo assim temos:
O momento de inércia da esfera é , assim temos:
Guarda essa expressão!
Agora nossa missão é encontrar a velocidade do platô.
Passo 2
O alcance da bola foi de , e podemos relacionar o tempo de queda com o deslocamento horizontal. Sabendo que a bola apenas tinha velocidade horizontal podemos calcular a velocidade dele. Mas pra isso precisamos do tempo! Vamos olhar o movimento na vertical então.
Da cinemática sabemos que o tempo de queda de um objeto em queda livre partindo do repouso é:
Ou seja,
No nosso caso . Assim o tempo de queda foi:
Agora da cinemática horizontal, podemos calcular a velocidade:
Agora sim vamos voltar lá pra equação do passo !
Passo 3
A expressão que econtramos foi:
Vou simplificar todas as massas e isolar :
Agora é só substituir os valores:
Show!
Bora treinar mais?