Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 6.Exercícios e Problemas - Ex. 22
Um jato Airbus A320 tem massa de durante a decolagem. Ele leva para atingir a velocidade de decolagem de (cerca de ). Qual é o empuxo dos motores? Você pode desprezar a resistência do ar, mas não o atrito de rolamento.
Passo 1
Vamos assumir que o avião é uma partícula acelerando em linha reta que está sob a influência de duas forças:
- O impulso de seus motores, (que é o que queremos saber);
- E a força de atrito de rolamento das rodas na pista,
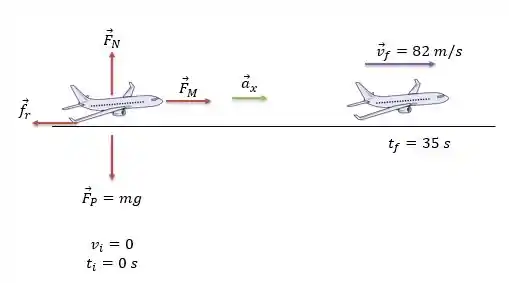
Além dessas duas forças na direção , sentido do movimento, temos a força peso e a força normal, que atuam na direção , na vertical.
O avião parte no tempo , com velocidade e atinge uma velocidade no tempo . Para que a velocidade do avião aumente deve existir uma aceleração no sentido do movimento, belezinha?
Passo 2
Para acharmos o valor dessa aceleração vamos fazer:
A segunda lei de Newton nos diz que:
Para esse caso:
Substituindo:
Então:
Substituindo o valor de :
Passo 3
Nosso próximo passo é achar quem é . Pela fórmula de força de atrito temos que:
Para uma borracha rolando no concreto (que é o caso da roda do avião rolando na pista):
Esse valor é encontrado na Tabela 6.1 do livro.
Mas ainda precisamos encontrar o módulo da força normal. O avião não se movimenta na direção , então o somatório de forças nessa direção tem que ser zero:
Agora podemos substituir:
Passo 4
Vamos retornar à equação que encontramos no passo 2:
E substituir o valor de :
A massa do avião foi fornecida na questão e a aceleração da gravidade a gente conhece né:
Logo:
Resposta
O empuxo dos motores é .