Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 97

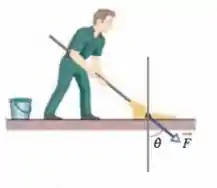
Na Fig. 6-61, um faxineiro caprichoso limpa o piso aplicando ao cabo do esfregão uma força F → . O cabo faz um ângulo θ com a vertical e μ s e μ k são os coeficientes de atrito estático e cinético entre o esfregão e o piso. Ignore a massa do cabo e suponha que toda a massa m do esfregão está concentrada no pano de chão. (a) Se o pano de chão se move ao longo do piso com velocidade constante, qual é o valor de F ? (b) Mostre que se θ for menor que um certo valor θ 0 , a força F → (ainda orientada ao longo do cabo) será insuficiente para fazer o pano de chão se mover. Determine θ 0 .

Passo 1

Esta é uma questão de aplicação direta da segunda lei de Newton. Para tanto, vamos considerar que o nosso semieixo x positivo esteja orientado para direita e o nosso semieixo y positivo esteja orientado para cima. Assim, aplicando a segunda lei de Newton a cada eixo e lembrando que em ambos os eixos a aceleração é nula:

e i x o   x :       F sin ⁡ θ - f k = 0       e q . 1

e i x o   y :       N - P - F cos ⁡ θ = 0       e q . 2

Lembrando também que a força de atrito cinético pode ser calculada através da seguinte relação:

f k = μ k N       e q . 3

Passo 2

Isolando a normal na e q . 2 :

N = m g + F cos ⁡ θ

Substituindo na e q . 3 :

f k = μ k m g + μ k F cos ⁡ θ

E, agora, substituindo na e q . 1 :

F sin ⁡ θ - μ k m g - μ k F cos ⁡ θ = 0

Por fim, isolando F :

F = μ k m g sin ⁡ θ - μ k cos ⁡ θ       e q . 4

Passo 3

Para fazer o pensamento desta parte da questão, devemos perceber que ao aplicar a segunda lei de Newton, porém, agora, considerando o equilíbrio EM REPOUSO, passaremos apenas a usar a força de atrito estático no lugar da força de atrito cinético. Assim, podemos usar diretamente a e q . 4 substituindo o μ k pelo μ s . Isso aconteceu, porque, para o caso anterior analisado, também fizemos a consideração do equilíbrio. Portanto:

F = μ s m g sin ⁡ θ - μ s cos ⁡ θ

Para continuar, devemos perceber que quanto menos o denominador desta fração, maior seria a força para mantê-lo em equilíbrio. Portanto, podemos determinar o ângulo que a força F → não movimentará o pano igualando o denominador a zero. Assim:

sin ⁡ θ 0 - μ s cos ⁡ θ 0 = 0

μ s = sin ⁡ θ 0 cos ⁡ θ 0 = tan ⁡ θ 0

Isolando o θ 0 :

θ 0 = tan - 1 ⁡ μ s

Portanto, para qualquer ângulo inferior a θ 0 = tan - 1 ⁡ ( μ s ) , o pano permanecerá em repouso.

Resposta

  1. F = μ k m g sin ⁡ θ - μ k cos ⁡ θ ;
  2. θ 0 = tan - 1 ⁡ ( μ s ) .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O bloco A da Figura 5.64 pesa 1,20N e o blocoB pesa 3,60N . O coeficiente de atrito cinético entre todas as superfícies é 0,300 . Determine o módulo da força horizontal F → necessária para arrastar o
O bloco A da Figura 5.63 pesa 60,0 N. O coeficiente de atrito estático entre o bloco e a superfície sobre a qual ele se apóia é de 0,25. O peso p é igual a 12,0 N, e o sistema está em equilíbrio. Calc
No sistema indicado na Figura 5.54, o bloco A possui massa m A e o bloco B possui massa m B e a corda que liga os blocos possui massa diferente de zero mcorda. A corda possui comprimentototal L e a po
Um bloquinho de massa igual a 100g encontra-se numa extremidade de uma prancha de 2m de comprimento e massa 0,5 Kg. Os coeficientes de atrito estático e cinético entre o bloquinho e a prancha são, res
Um bloco está numa extremidade de uma prancha de 2m de comprimento. Erguendo-se lentamente essa extremidade, o bloco começa a escorregar quando ela está a 1,03 m de altura, e então leva 2,2s para desl