Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 3.Problemas - Ex. 47
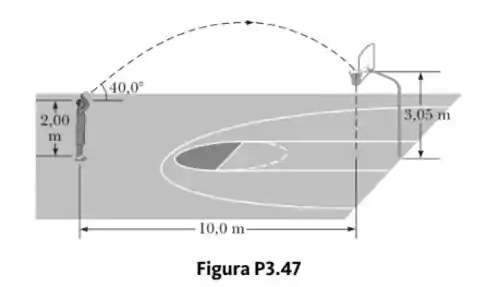
Um jogador de basquete está em pé a 10,0 m da cesta, conforme a Figura P3.47. A altura da cesta é de 3,05 m, e ele lança a bola a um ângulo de 40,0° com a horizontal, a uma altura de 2,00 m.
(a) Qual é a aceleração da bola de basquete no ponto máximo da sua trajetória?
(b) Com que velocidade o jogador deve lançar a bola para que passe pelo aro sem bater na tabela?
Passo 1
(a) Amores, pelo lançamento oblíquo da bola, ela vai ter aceleração centrípeta devido ao movimento curvilíneo. Em todos os pontos da trajetória, essa centrípeta vai ser devida à componentes da aceleração da gravidade, apontando na direção radial da curva sempre!
Nisso, inclusive no ponto máximo da trajetória a aceleração que a bola sofre vai ser a aceleração da gravidade, nesse caso, valendo o valor exato de .
Passo 2
(b) Seguinte, gente, como a gente já viu de exercícios anteriores, nos lançamentos oblíquos, a componente horizontal da velocidade do objeto é sempre constante: é um movimento uniforme.
Nisso, considerando a distância entre a posição inicial da bola e a cesta sendo , vale a gente escrever que:
Ah, , a velocidade original da bola e se correlacionam pelo seguinte esqueminha, já usado outras vezes ao longo do capítulo:
Com isso, a gente tem que , blz??
Ok! Se a gente determinar , ou pelo menos alguma expressão pra , o tempo da bola sair da mão do jogador até cair na cesta, determinamos a velocidade original do lançamento!
Passo 3
O melhor pra gente nesse caso é trabalhar com a equação do sorvetão:
Aqui, , a posição final da bola, vai ser (altura da cesta); , altura de onde a bola parte (mãos do jogador); é a velocidade vertical inicial da trajetória da bola, e finalmente , a gravidade, beleza?
Só aplicar e a gente vai ter:
Aqui a gravidade leva sinal negativo pra indicar que a trajetória inicial da bola segue o sentido oposto da gravidade, beleza?
Seguindo em frente:
Ok. Aqui, o que a gente vai fazer?
Lá no Passo 1 a gente chegou à seguinte equaçãozinha:
A partir disso, a gente tem pra que:
Vamos então substituir na equação quadrática que a gente chegou por essa expressãozinha, tudo bem?
Ficamos assim:
Passo 4
Legal, a gente tem agora uma expressão cuja única incógnita é , a velocidade original de lançamento que a gente queria, a princípio!
Vamos trabalhar ela mais um pouco, realizando a soma das frações. A partir do MMC dos denominadores, a gente vai ter isso aqui:
Multiplicamos em cruz e procedemos o produto dentro dos parênteses, obtendo:
Vamos juntar os termos em comum em um mesmo lado da igualdade e colocar o possível em evidência:
Com isso, a gente pode isolar do restante, assim:
Maravilha! Agora, dados os valores de e com 3 casas após a vírgula pela calculadora, a gente vai ter o seguinte: