Um jogador chuta uma bola de futebol com velocidade inicial cujo componente vertical é e o componente horizontal é . Despreze a resistência do ar. (a) Quanto tempo a bola leva para atingir a altura máxima de sua trajetória? (b) Qual a altura desse ponto? (c) Quanto tempo a bola leva (desde o momento do chute inicial) até o instante em que ela retorna ao mesmo nível inicial? Qual é a relação entre esse tempo e o calculado no item (a)? (d) Que distância horizontal ela percorreu durante esse tempo? (e) Faça diagramas , , e para o movimento.

Letra a:

Vamos começar usando a equação horária da velocidade:

Onde é componente vertical da velocidade da bola, é sua velocidade inicial e o tempo.

Então, isolando o tempo na equação, vamos ter o tempo que a bola leva para atingir a altura máxima de sua trajetória:

Letra b:

Diferentes equações de aceleração constante fornecem expressões diferentes, mas o mesmo resultado numérico. Então, podemos fazer:

ou

E obter:

Letra c:

Independentemente de como a álgebra é feita, o tempo que a bola leva (desde o momento do chute inicial) até o instante em que ela retorna ao mesmo nível inicial será o dobro do encontrado na parte (a), que é:

Letra d:

Agora para calcular a distância horizontal percorrida pela bola, vamos considerar e usar a equação:

Onde é a velocidade horizontal inicial e é a variação da posição. Assim, temos:

Letra e:

Agora esboçando os diagramas , , e para o movimento, temos:

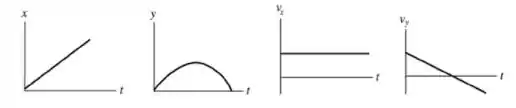
Quando a bola de futebol retorna ao seu nível original,

Valeu, galera! Até a próxima! 😉