Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 79
79. Em uma competição rural, uma mola lança uma bola com velocidade de a partir de um canto de uma mesa plana e regular inclinada 20° acima da horizontal. Para vencer, o jogador deve fazer com que a bola atinja um pequeno alvo situado no canto adjacente da tábua, a de distância. Em que ângulo " com a horizontal o jogador deve posicionar a mola lançadora?
Passo 1
E aí senhores! Aqui vamos nós de novo!
Essa é uma clássica questão sobre lançamentos!
E pra resolver esse tipo de questão, já sabe né?
Primeiro bora fazer um esboço pra ajudar a entender melhor o nosso problema...
Aqui está nosso belo desenho;
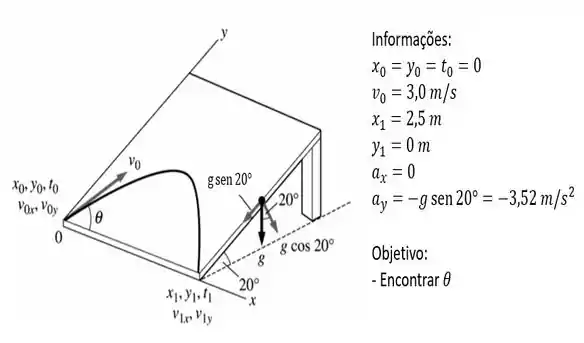
Passo 2
Bom! Tomando como o instante inicial do movimento da bola, as suas componentes de velocidade nesse momento são dadas por...
Passo 3
Sendo assim, pra facilitar a nossa resolução, bora dividir o movimento da bolinha em duas partes, vertical e horizontal...
Na horizontal, em , nossa bola não tem aceleração influenciando seu movimento. Sendo assim, ela executa um movimento uniforme, com velocidade constante.
Olhando pra nossa figura, ficamos então com...
E substituindo os valores numéricos de cada variável;
Podemos descobrir o tempo de movimento da bola, isolando ...
E como ;
Passo 4
Indo agora pra direção vertical, temos nessa direção a presença da aceleração da gravidade para baixo influenciando o deslocamento da bolinha.
Desse modo, peguemos a equação abaixo para o movimento uniformemente variado... É claro, usando as variáveis da nossa figura, né!?
Esse é a componente da nossa nossa aceleração da gravidade, com sentido negativo, uma vez que aponta para baixo e segundo a figura que desenhamos, dada por .
Desse modo, substituindo os valores conhecidos...
E cortando dos dois lados no denominador...
Ficamos com a relação acima... Onde substituindo os valores pertencentes a cada variável;
Finalmente obtemos o valor do nosso ângulo de lançamento.