Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 8.Problemas - Ex. 100
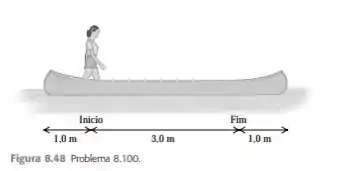
Uma jovem de está em pé sobre uma canoa de e comprimento igual a . Ela caminha a partir de um ponto situado a de uma das extremidades da canoa até atingir a outra extremidade da canoa (Figura ). Desprezando a resistência da água ao movimento da canoa, qual a distância que a canoa se move nesse processo?
Passo 1
Fala, galerinha! Beleza? Vamos resolver mais essa?
O enunciado pediu pra gente determinar a distância que a canoa se move durante a caminhada da jovem.
Sabemos inicialmente que a jovem e a canoa estão paradas, portanto o centro de massa do sistema está localizado em um certo ponto com uma velocidade igual a zero, .
Assumindo como sendo para direita por conservação de momento, temos que o momento final do sistema também deve ser zero, logo em nenhum momento o centro de massa do sistema se move.
Portanto, o centro de massa do sistema inicialmente será:
Como o centro de massa não se desloca, temos então que após a jovem se deslocar que a posição do centro de massa é:
A partir dessas duas equações, vamos determinar o deslocamento , onde é a posição inicial da canoa e sua posição final.
Vamos lá!
Passo 2
Como a posição do centro de massa do sistema permanece o mesmo, temos .
Assim, igualando as equações que vimos no passo anterior, teremos:
Simplificando os denominadores, ficamos com:
Agora vamos substituir os valores!
Passo 3
Temos que o centro de massa da canoa apenas fica localizado na metade do seu tamanho, ou seja,
Portanto a jovem caminha até uma posição de após o centro de massa. Logo, temos que a posição da jovem será em
Assim, substituindo os valores que temos na equação, temos que:
Resolvendo isso, temos:
Porém, o problema nos pergunta quanto a canoa deslocou. Logo o resultado será
Valeu, galera! Até a próxima! 😉