Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 8.1 - Ex. 13
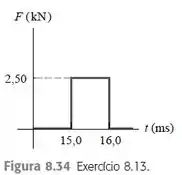
Uma pedra de está deslizando a da esquerda para a direita sobre uma superfície horizontal sem atrito, quando é repentinamente atingida por um objeto que exerce uma grande força horizontal sobre ela, por um curto período de tempo. O gráfico na mostra o módulo dessa força em função do tempo.
(a) Qual é o impulso que essa força exerce sobre a pedra?
(b) Imediatamente após a força cessar, ache o módulo, a direção e o sentido da velocidade da pedra se a força atuar
(i) para a direita e
(ii) para a esquerda.
Passo 1
Show de bolinhas galera! O problema nos deu um gráfico de , com isso o impulso pode ser calculado a partir da área do gráfico.
Como a área é um retângulo, podemos calcular sem problemas (caso seja uma figura estranha, daí só integrando!). Calculando a área embaixo da curva, encontraremos o nosso impulso.
Passo 2
- A área embaixo dessa curva é dada como:
- Belezera, agora i) Se a força atuar para a direita, vai estar no mesmo sentido da velocidade inicial, assim temos que:
Portanto o impulso será:
Logo:
O valor do impulso nós já calculamos e ele vai ser positivo, o valor da massa e da velocidade inicial foram dados, então agora é só substituir para achar a velocidade final, sendo assim:
Então a velocidade final vai ser para a direita.
Passo 3
ii) Agora mudando o sentido da força, mudamos o sentido do impulso. Ele possui o mesmo módulo, mas agora vai ser negativo. Os outros dados não mudam, então agora é só substituir na fórmula:
Logo:
Agora a velocidade final vai ser para a direita.
