Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 14.Problemas - Ex. 59
Uma barca aberta possui as dimensões indicadas na Figura 14.38. Sabendo-se que todas as partes da barca são feitas com placas de aço de espessura igual a 4,0 cm, qual é a massa de carvão que a barca pode suportar em água doce sem afundar? Existe espaço suficiente na parte interna da barca para manter essa quantidade de carvão? (A densidade do carvão é aproximadamente igual a .)
Passo 1
Vamos aplicar a Segunda lei de Newton à barcaça e seu conteúdo. Aplicaremos o princípio de Arquimedes para expressar a força de flutuação B em termos de volume da barcaça.
Vamos esboçar o diagrama de corpo livre para a barcaça mais o carvão:
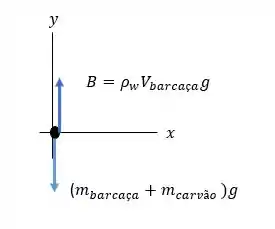
Passo 2
Assim, podemos executar:
A massa da barcaça é , onde refere-se ao aço.
Passo 3
Da Tabela 14.1,
O volume vezes a área total das cinco peças de aço que compõem a barcaça:
Portanto,
Então
O volume dessa massa de carvão é
isso é menos que , assim caberá na barcaça.
A força de flutuação B deve suportar o peso do carvão e também o peso da barcaça. O peso do carvão é cerca de 13 vezes o peso da barcaça. A força de flutuação aumenta quando mais da barcaça está submersa; portanto, quando retém a massa máxima de carvão, a barcaça fica totalmente submersa.
Resposta
caberá na barcaça