Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 3.Problemas - Ex. 15
Uma casca uniformemente carregada com densidade volumétrica contém em seu interior uma cavidade esférica. Mostre que o campo no interior da cavidade é uniforme e é dado por
onde é o vetor que liga os centros das duas esferas (fig.).
Sugestão: Use o princípio da superposição.
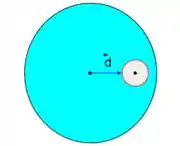
Passo 1
Se liga! Podemos começar calculando o campo em toda esfera desprezando a cavidade.
Para isso usaremos uma superfície superfície gaussiana com simetria esférica. Veja a figura.
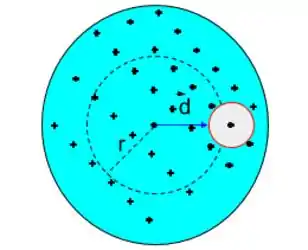
Só precisamos aplica a lei de Gauss
A área é a área da esfera da superfície gaussiana
A carga é a carga localizada dentro da esfera gaussiana
Isso nos da um campo
Como o campo aponta para fora na direção radial
Passo 2
Agora vamos calcular o campo dentro da cavidade, beleza?!
Vamos considerar que a casca está carregada negativamente de modo que somando-a a esfera, a carga se anulará.
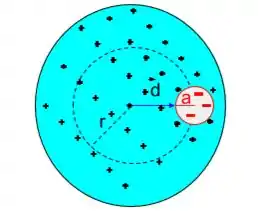
O campo produzido pela cavidade, de forma análoga ao que acabamos de fazer para a esfera será
Se repararmos na imagem, podemos ver que
Passo 3
Agora só precisamos fazer a soma dos campos
Sendo assim, podemos perceber que o campo é uniforme e depende apenas do vetor .