Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 5.1 - Ex. 118
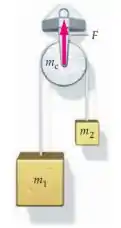
Na máquina de Atwood abaixo a corda passa por cima do cilindro fixo de massa . O cilindro não roda. Ao invés disso, a corda desliza sobre a sua superfície sem atrito. (a) Encontre a aceleração do centro de massa do sistema blocos-cilindro-corda. (b) Use a segunda lei de Newton para sistemas para encontrar a força exercida pelo suporte. (c) Encontre a tensão na corda conectando os blocos para mostrar que .
Passo 1
(a) Olá, querido, tá bem? Temos essa peça formada pelos blocos, o fio e o cilindro. Ele quer saber a aceleração do centro de massa desse conjunto.
A expressão da aceleração do centro de massa é
Onde é a massa total do conjunto, é a aceleração do centro de massa e é a soma do produto entre massa e velocidade para cada parte do nosso conjunto.
No nosso caso, a expressão para a aceleração do centro de massa fica da seguinte forma:
A massa total é a soma das massas dos blocos e do cilindro (vamos desprezar a massa da corda), então fica:
E temos que a aceleração do cilindro é nula porque ele fica parado, e temos que a aceleração dos blocos vai ser igual porque eles estão ligados por um fio. Chamando essa aceleração de , ficamos com:
Isolando quem a gente quer:
Passo 2
Agora precisamos encontrar uma expressão para a aceleração dos blocos. Para fazer isso, vamos aplicar a segunda lei de Newton na vertical em cada bloco. Tá aqui o diagrama de corpo livre desses dois carinhas:
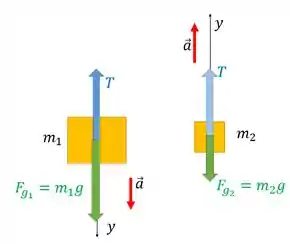
Para cada bloco colocamos um referencial diferente, mas nos dois casos ele está positivo no sentido da aceleração para facilitar nossas contas.
Para o bloco da direita podemos escrever a seguinte expressão da segunda lei de Newton:
E para o bloco da esquerda:
Somando as duas equações e
E substituindo isso na expressão do passo anterior:
Passo 3
(b) Ele quer . Olhando para o sistema inteiro, as únicas forças externas em ação são a força do suporte e o peso total do sistema, então podemos escrever a segunda lei de Newton para o conjunto formado pelos blocos, corda e cilindro:
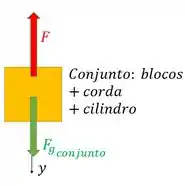
Mais uma vez colocamos o sistema positivo no sentido da aceleração do centro de massa do conjunto (ela está para baixo porque o bloco maior está caindo). A segunda lei de Newton fica:
Lembrando que a aceleração aqui é aceleração do centro de massa que a gente já achou. Continuando:
Lembrando que é a massa total do conjunto e substituindo nossa expressão de :
Agora vamos tentar simplificar um pouco essa expressão
Passo 4
(c) Queremos . Vamos voltar ao sistema de equações que montamos no passo :
E agora vamos subtrair a segunda equação da primeira:
E substituindo a expressão que já temos para (Aceleração dos blocos) lá do passo 2 também:
Agora vamos simplificar um pouco essa expressão abrindo os produtos notáveis:
Passo 5
E podemos demonstrar a relação que foi pedida se substituirmos isso no resultado que encontramos no item (b):
Rearrumando:
Vimos no passo anterior que
Substituindo isso na equação acima na parte dentro do parênteses mais interno
E então:
Que é o que ele pede!
Resposta
(a) .
(b) .
(c)
.