A extremidade inferior de uma mola vertical, sem massa, e com constante de força repousa sobre uma balança, e a extremidade superior está presa a um copo sem massa, como na figura. Posicione uma bola de massa gentilmente dentro do copo até deixa-la em uma posição de equilíbrio. (a) Desenho o digramas de corpo livre separados para a bola e para a massa. (b) Mostre que, nessa situação, a compressão da mola é dada por . (c) Qual é a leitura da balança sob essas condições?

Passo 1
(a) Vamos começar com os diagramas de corpo livre, lembrando que queremos considerar que a mola não tem massa:
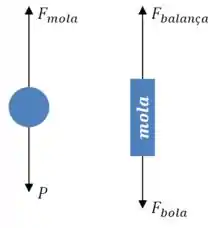
E nesse desenho, , por exemplo, representa a força exercida pela mola sobre o corpo em questão.
Passo 2
(b) Vamos considerar que as forças verticais que agem sobre a bola estão em equilíbrio:
A força que a mola exerce sobre a bola pode ser calculada pela lei de Hooke:
E então o deslocamento da mola nesse instante é:
Passo 3
(c) Uma forma rápida de resolver essa questão é pensar o seguinte: pela terceira lei de Newton, a força que a bola faz sobre a mola tem o mesmo módulo da força que a mola faz sobre a bola.
Essas duas forças são internas do sistema. A única força externa agindo sobre o corpo, e contra a qual a balança exercerá uma reação normal (que é justamente aquilo que sua leitura indica), é o peso da bola:
O que é um resultado bastante intuitivo, consdeirando que a mola e o copo não têm massa.
Resposta
(a) Desenho.
(b) .
(c) A leitura da balança é .