Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 1.7 - Ex. 25

A massa específica do ferro é 7,87 g / c m 3 e a massa de um átomo de ferro é 9,27 * 10 - 26   k g . Se os átomos são esféricos e estão densamente compactados,

(a) qual é o volume de um átomo de ferro

(b) qual é a distância entre os centros de dois átomos vizinhos?

Passo 1

O primeiro conceito que devemos dominar para resolver essa questão é o da massa específica. Podemos achar a massa específica de um elemento através da relação ;

ρ = m v

Onde ,

m = massa de uma porção do elemento

v = volume de uma porção do elemento

Logo ,

7,87 g c m 3 = 9,27 * 10 - 26 k g v

v = 9,27 * 10 - 23 g * c m 3 7,87 g = 1,18 * 10 - 23 c m 3 = 1,18 * 10 - 29 m 3

Passo 2

A primeira coisa que devemos fazer é entender geometricamente o que significa a distância entre os centros de 2 átomos vizinhos :

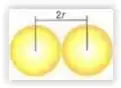
Agora podemos visualizar que essa distância coincide com o valor do diâmetro , ou seja , 2 vezes o valor do raio. O raio , por sua vez , pode ser calculado através da relação:

v = 4 π r 3 3 = 1,18 * 10 - 29 m 3

r = 3 * 1,18 * 10 - 29 4 π 1 3

r = 1,41 * 10 - 10   m

A distância entre os centros é de 2,82 * 10 - 10   m !!

Essa foi de boa ,né? Vamos para o próximo exercício!!!!

Resposta

  1. 1,18 * 10 - 29 m 3
  2. 2,82 * 10 - 10   m !!
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um metro cúbico ( 1,00m 3 ) de alumínio tem massa de 2,70 × 10 3k g , e o mesmo volume de ferro tem massa de 7,86 × 10 3k g . Encontre o raio de uma esfera de alumínio maciço que equilibrará uma esfer
Suponha que leve 7,00m i n para encher um tanque de gasolina de 30,0g a l . Calcule a taxa à qual o tanque é enchido em galões por segundo. Calcule a taxa à qual o tanque é enchido em metros cúbicos p
Represente por ρ A l a densidade do alumínio e ρ F e a do ferro. Encontre o raio de uma esfera de alumínio maciço que equilibra uma esfera maciça de ferro de raio r F e em uma balança de braços iguais
Um átomo de hidrogênio tem diâmetro de 1,06 × 10 - 10m . O núcleo desse átomo tem diâmetro de aproximadamente 2,40 × 10 - 15m . Para um modelo em escala, represente o diâmetro do átomo de hidrogênio p
O ano tropical, intervalo de tempo entre um e outro equinócio vernal, é a base de nosso calendário. Ele contém 365,242199d i a s . Encontre o número de segundos em um ano tropical.