Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 83
Se uma das massas da máquina de Atwood da Figura 4-60 é , quanto deve valer a outra massa de forma a que o deslocamento de cada massa, durante o primeiro segundo após a largada, seja Suponha uma polia sem massa e sem atrito e um fio sem massa.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Está exposto abaixo o diagrama de corpo livre dos dois blocos:
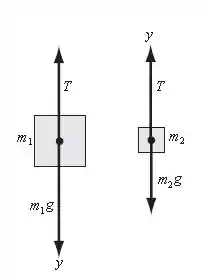
É possível notar que em cada bloco foi considerado um sistema de coordenadas diferente, e isto foi feito justamente para melhorar o entendimento nos cálculos.
Passo 2
Aplicando a segunda lei de Newton no bloco de massa temos:
Aplicando a segunda lei de Newton no bloco de massa temos:
Como os blocos estão conectados pela polia simples, temos uma aceleração única para os dois corpos:
Substituindo, temos:
Relacionando as duas equações, temos:
Passo 3
Usando a equação da posição para aceleração constante, temos:
Substituindo os valores, temos:
Agora que encontramos a aceleração dos corpos, podemos encontrar a massa .
Se , temos que:
Se , temos que:
Resposta
O objeto pode ter massa de ou .