Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 93
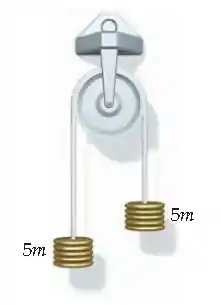
As massas penduradas nos dois lados de uma máquina de Atwood ideal consistem em uma pilha de cinco arruelas, cada uma de massa , como mostrado na Figura 4-65. A tensão no fio é . Quando uma das arruelas é retirada do lado esquerdo, as demais arruelas aceleram e a tensão é reduzida em . (a) Encontre (b) Encontre a nova tensão e a aceleração de cada massa quando uma segunda arruela é retirada do lado esquerdo.
Passo 1
a) Olá, querido! Tá bem? Seguinte, vamos tentar entender o que houve aí.
O primeiro momento é esse onde temos uma polia, e presas ao dois lados das cordas temos massas iguais. Por causa disso, elas se equilibram, e esse sistema está parado. Ou seja, ambos os lados tem aceleração .
Então, nesse caso, a tensão em um lado da corda vai ser a força necessária para manter um objeto de massa parado.
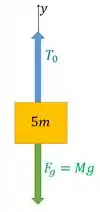
Então, essa tensão precisa ser igual a força peso sobre o objeto que o puxa para baixo, ou seja:
A tensão é a mesma em todos os pontos de uma corda, então vale para toda a corda.
Só que uma massa é tirada do objeto do lado esquerdo, então há um desequilíbrio, fazendo com que a tensão diminua
A partir disso, ele quer saber o valor de . Bora lá!
Passo 2
O diagrama de corpo livre de cada objeto preso a corda após o equilíbrio está exposto abaixo:
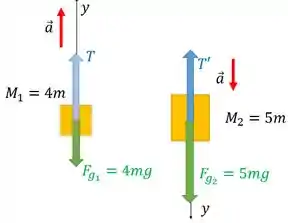
Vê que a colocamos diferente em cada objeto, no sentido da aceleração, para facilitar nossas contas. O objeto mais pesado vai puxar o outro em sua direção.
Aplicando a segunda lei de Newton para o carinha da esquerda, temos:
Para o carinha da direita:
Passo 3
Como e é a mesma para os dois objetos, porque a corda é a mesma para os dois e eles se movem juntos a ela, temos duas equações relacionando e , um sistema:
Isolando nas duas e igualando:
Isolando que é a única variável que sobrou:
Substitiundo isso na equação e isolando :
Podemos substituir isso na equação que fizemos para lá no passo 1:
Isolando (que a gente quer achar desde o ínicio) e substituindo :
Passo 4
Item (b):
Podemos seguir o caminho do item anterior para a nova situação:
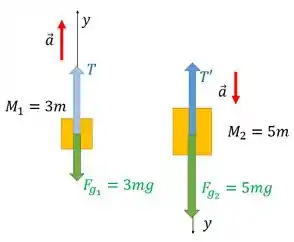
Aqui o objeto do lado esquerdo perdeu uma massa . A segunda lei de Newton para ele fica:
E para o objeto da direita fica:
Como , vamos isolar e nessas duas equações e igualar para achar :
Susbtituindo os valores, temos que:
Passo 5
Para achar a tensão, a gente pode substituir essa aceleração na equação da segunda lei de Newton do cara da esquerda:
Isolando :
Susbtituindo os valores, temos que: