Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 85
Um seixo de massa está sobre o bloco de massa da máquina de Atwood ideal da Figura 4-60. Encontre a força exercida pelo seixo sobre o bloco de massa .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O diagrama de corpo livre do problema está exposto na figura abaixo:
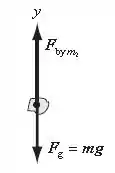
Aplicando , temos:
Do problema 82, temos:
Aplicando ao nosso problema, com um seixo de massa , temos:
Substituindo na equação da força, temos:
Resposta
Exercícios de Livros Relacionados
Um bloco B de massa de 5k g está sobre um bloco A de massa de 8k g , que por sua vez está sobre o topo de uma mesa horizontal (Figura 5.72 ). Não há atrito entre o bloco A e o topo da mesa, mas o coef
Dois blocos estão conectados por uma corda que passa sobre uma polia fixa sem atrito e repousam sobre planos inclinados (Figura 5.70 ). a) Como os blocos devem se mover quando forem soltos a partir do
O problema do macaco e das bananas. Um macaco de 20k g segura firmemente uma corda que passa sobre uma polia sem atrito e está amarrada a um cacho de bananas com 20k g (Figura 5.77 ). O macaco olha pa
Dois objetos com massas de 5,0k g e 2,0k g estão suspensos a 0,600m acima do solo presos nas extremidades de uma corda de 6,0m que passa sobre uma polia fixa sem atrito. Os dois objetos partem do repo
Acelerômetro. A Figura 5.76 mostra um sistema que pode ser usado para medir a sua aceleração. Um observador que caminha sobre a plataforma mede o ângulo θ que o fio que sustenta a bola leve forma com