Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 86

Um acelerômetro simples pode ser feito suspendendo-se um pequeno objeto massivo em um fio preso a um ponto fixo de um objeto acelerado. Um acelerômetro como este está preso em um ponto P do teto de um automóvel viajando em linha reta sobre uma superfície plana com aceleração constante. Devido a aceleração, o fio formará um ângulo θ com a vertical. (a) Mostre que a magnitude da aceleração a está relacionada com o ângulo θ por a = g tan ⁡ θ .   (b) Se o automóvel freia uniformemente de 50   k m / h até o repouso, ao longo de uma distância de 60 m, qual é o ângulo que o fio formará com a vertical? Durante o fretamento, o objeto suspenso estará posicionado abaixo e à frente ou abaixo e para trás do ponto P ?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O diagrama de corpo livre do problema está exposto na figura abaixo:

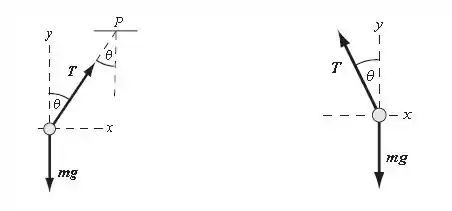
Aplicando ∑ F → = m a → , temos:

∑ F x = m a x

T sin ⁡ θ = m a x

∑ F y = m a y

T cos ⁡ θ - m g = 0

Relacionando as duas equações, temos que:

T sin ⁡ θ T cos ⁡ θ = m a x m g

tan ⁡ θ = a x g

Logo:

a x = g tan ⁡ θ

Passo 2

O item (b) nos pede o ângulo formado a partir das condições fornecidas no enunciado. Do passo 1, temos que:

tan ⁡ θ = a x g

Logo:

θ = tan - 1 ⁡ a x g

Como nos foi fornecida a velocidade, podemos usar a equação de torricelli para descobrir a aceleração desconhecida. Temos que:

v x 2 = v 0 x 2 + 2 a x ∆ x

Como a velocidade final é nula, temos que:

0 = v 0 x 2 + 2 a x ∆ x

a x = - v 0 x 2 2 ∆ x

Portanto:

θ = tan - 1 ⁡ - v 0 x 2 2 ∆ x g

θ = tan - 1 ⁡ - v 0 x 2 2 g ∆ x

Substituindo os valores, temos:

θ = tan - 1 ⁡ - 50 k m h ⋅ 1   h 3600   s ⋅ 1000   m 1   h 2 2 ⋅ 9,81 m s 2 ⋅ 60   m

θ = 9,3 °

Resposta

a ) a x = g tan ⁡ θ

b ) θ = 9,3 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pequeno foguete de 8 k g queima combustível que exerce uma força de baixo para cima, que varia com o tempo, sobre o foguete. Essa força obedece à equação F = A + B t 2 . Medidas mostram que no inst
Uma carreta de brinquedo pesando 4,5 k g está em aceleração por uma linha reta ( e i x ox ) . O gráfico da figura 4.33 mostra essa aceleração em função do tempo. Ache a força resultante máxima que atu
Um elétron ( m a s s a = 9,11 × 10 - 31 k g ) deixa a extremidade de um tubo luminoso de TV com velocidade inicial igual a zero e se desloca em linha reta até a grade de aceleração, que está a uma dis
Um disco de hóquei com massa de 0,160 k g está em repouso na origem ( x = 0 ) em uma superfície horizontal sem atrito da pista. No instante t = 0 , um jogador aplica sobre o disco uma força de 0,250 N
Um gato de 2,75 k g move-se em linha reta ( e i x ox ) . A figura 4.34 mostra um gráfico do componente x da velocidade desse gato em função do tempo. Ache a força resultante máxima que atua nesse gato