Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 92

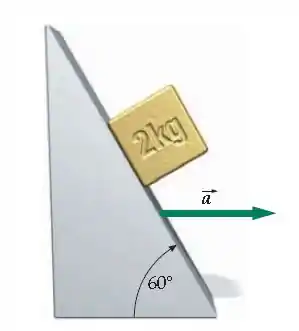
Um bloco de está sobre uma cunha sem atrito que tem uma inclinação de e uma aceleração para a direita, de tal forma que a massa permanece estacionária em relação à cunha (Figura 4-64). (a) Desenhe o diagrama de corpo livre do bloco e use-o para determinar a magnitude da aceleração. (b) O que aconteceria se a cunha recebesse uma aceleração maior que este valor? E menor?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O diagrama de corpo livre do sistema está exposto abaixo:

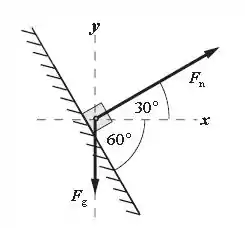
Aplicando a segunda lei de Newton, temos:

Como o corpo está estacionário , logo:

Dividindo as duas equações, temos:

Passo 2

Item (b):

Pensa comigo, se tivermos uma aceleração maior que , quer dizer que a força normal deve ser maior que a componente do peso em

Sob esta condição, teremos uma força resultante para cima, portanto o corpo irá acelerar para cima.

Se a aceleração for menor que a encontrada, então a força normal será:

Sob esta condição, teremos uma força resultante para baixo, portanto o corpo irá acelerar para baixo.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Figura P4.53, o plano inclinado tem massa M e é fixado ao tampo da mesa horizontal fixa. O bloco de massa m é colocado próximo à base do plano inclinado e é solto com um impulso rápido que o faz de

Um bloco desliza para baixo em um plano sem atrito com uma inclinação de θ=15,0 ° . O bloco parte do repouso no topo e o comprimento da rampa é de 2,00m . Desenhe um diagrama de corpo livre do bloco.

Um carro acelera descendo uma colina (Fig. P4.57), partindo do repouso a 30,0m / s em 6,00s . Um brinquedo dentro do carro está pendurado por um fio no teto. A bola na figura representa o brinquedo de

Um bloco de massa m=2,00k g é liberado do repouso a h=0,500m acima da superfície de uma mesa, no topo de um plano inclinado com θ=30,0 ° , conforme mostrado na Figura P4.53. O plano inclinado é fixado

Um plano sem atrito tem 10,0m de comprimento e 35,0 ° de inclinação. Um trenó começa na parte de baixo com velocidade inicial de 5,00m / s subindo o declive. Quando ele alcança o ponto no qual momenta