Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 74
Uma bala de canhão é disparada com uma rapidez inicial a um ângulo de 30° acima da horizontal, de uma altura de 40 m acima do chão. O projétil chega ao chão com uma rapidez de . Encontre (Ignore a resistência do ar.)
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O movimento descrito no enunciado está representado na figura abaixo:
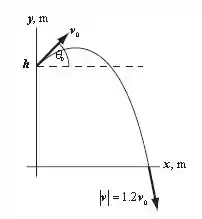
Podemos expressar as componentes da velocidade por:
Como temos informações sobre altura e velocidade, mas não nos é informado nada sobre o tempo do movimento, podemos aplicar Torricelli:
Sabemos que:
Logo:
Substituindo:
Sabemos que, , portanto:
Substituindo os valores, temos:
Resposta
Exercícios de Livros Relacionados
Uma bola é lançada a partir do solo com uma certa velocidade. A Fig. 4-45 mostra o alcance R em função ao ângulo de lançamento θ 0 . O tempo de percurso depende do valor de θ 0 ; seja t m á x á , o ma
Um rebatedor golpeia uma bola de beisebol quando o centro da bola está 1,22m acima do solo. A bola deixa o taco fazendo um ângulo de 45 ° com o solo e com uma velocidade tal que o alcance horizontal (
Em 1939 ou 1940 , Emanuel Zacchini levou seu número de bala humana a novas alturas: disparado por um canhão, passou por cima de três rodas-gigante antes de cair em uma rede (Fig.4-39). (a) Tratando Za
Na Fig. 4-44, uma bola de beisebol é golpeada a uma altura h=1,00m e apanhada na mesma altura. Deslocando-se paralelamente a um muro, passa pelo alto do muro 1,00s após ter sido golpeada e, novamente,
Quando vê um inseto pousado em uma planta perto da superfície da água, o peixe-arqueiro coloca o focinho para fora e lança um jato d'água na direção do inseto para derrubá-lo na água (Fig. 4-38). Embo