Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.Problemas Adicionais - Ex. 101
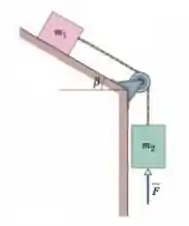
Na Fig. 5-61, uma lata de antioxidantes () sobre um plano inclinado sem atrito está ligada a uma lata de apresuntado (). A polia tem massa e atrito desprezíveis. Uma força vertical para cima de módulo atua sobre a lata de apresuntado, que tem uma aceleração para baixo de . Determine (a) a tensão da corda e (b) o ângulo .
Passo 1
Vamos iniciar esta questão fazendo o DCL dos dois blocos:
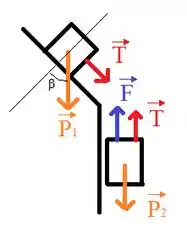
Nesta ilustração, podemos percerber que o único bloco que quando aplicado a segunda lei de Newton não vai precisar do ângulo parao cálculo é o bloco . Então, para determinarmos o módulo da tensão vamos usá-lo.
Passo 2
Aplicando a segunda lei de Newton para a componente do bloco :
Substituindo os valores conhecidos e isolando :
Passo 3
Para determinar o ângulo vamos aplicar a segunda lei de Newton para componente do bloco tendo em mente que a aceleração dos dois blocos é igual tendo em vista que se movem juntos. Além disso, como a polia é ideal, podemos afirmar que o módulo da tração também é igual. Assim:
Substituindo os valores conhecidos:
Isolando o :
Isolando o :
Resposta
- ;
- .