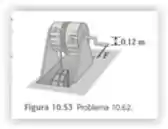
O mecanismo indicado na Figura 10.53 é usado para elevar um engradado de suprimentos do depósito de um navio. O engradado possui massa total de 50 kg. Uma corda é enrolada em um cilindro de madeira que gira em torno de um eixo de metal. O cilindro possui raio igual a 0,25 m e momento de inércia em torno do eixo. O engradado é suspenso pela extremidade livre da corda. Uma extremidade do eixo está pivotada em mancais sem atrito; uma manivela está presa à outra extremidade. Quando a manivela gira, sua extremidade gira em torno de um círculo vertical de raio igual a 0,12 m, o cilindro gira e o engradado sobe. Calcule o módulo da força aplicada tangencialmente à extremidade da manivela para elevar o engradado com uma aceleração de 0,80 m/s2. (A massa da corda e o momento de inércia do eixo e da manivela podem ser desprezados.)

Para a resolução do problema, vamos montar um esquema demonstrando as forças aplicadas

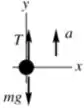
Como temos a força peso, a tensão e a aceleração, aplicaremos a segunda lei de Newton , para chegar a .

Essa lei permite o entendimento das forças mas não no sentido rotacional, por isso usaremos o momento angular no segundo momento, dado pelo diagrama:

Aplicando a segunda Lei de Newton,

Onde é força, é massa, é a aceleração, é a tração e é a aceleração da gravidade.

Agora lembrando da figura 10.62b, aplicaremos a fórmula de momento

Onde é o torque, é o momento de inércia e é a aceleração angular.

, onde l=0,12 m e R=0,25 m.

Como, , então .