Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 5.Problemas - Ex. 3
Mede-se a velocidade de propagação de ondas transversais num fio com uma extremidade presa a uma parede, que é mantido esticado pelo peso de um bloco suspenso da outra extremidade através de uma polia. Depois, mergulha-se o bloco na água até os da altura e verifica-se que a velocidade de propagação cai para da anterior, qual é a denisdade do bloco em relação á água?
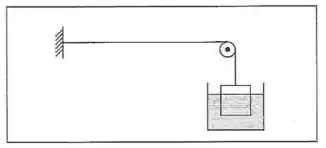
Passo 1
A velocidade de propagação da onda no fio segue a seguinte fórmula:
Nesse caso, a tensão é simplesmente o peso efetivo do bloco (ou seja, a força resultante que ele faz para baixo).
Inicialmente, quando o bloco não está imerso, tínhamos a seguinte relação:
Quando o peso efetivo muda para um valor novo, passamos a ter o seguinte:
Elevando os dois lados ao quadrado:
Passo 2
Podemos deduzir que o peso efetivo é um pouco menor por conta do empuxo produzido pelo fluido, que empurra o bloco para cima:
Substituindo isso na equação de cima:
Agora vamos escrever a massa do bloco como:
Onde é a densidade do bloco. E o empuxo sobre o bloco como:
Onde é a densidade da água. Então:
Passo 3
Podemos escrever o volume submerso do bloco como:
Se a altura submersa é da altura total, então:
Substituindo isso na nossa fórmula do passo anterior:
Resposta
A densidade do bloco é vezes a densidade da água.