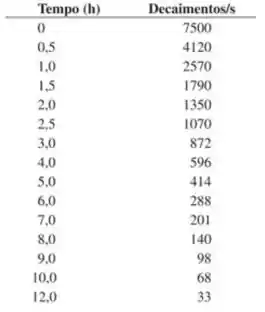
As medidas de atividade de uma amostra radioativa com diversos elementos misturados são indicadas na table abaixo. (a) Quantos nucleotídeos diferentes estão presentes na mistura? (b) Quais são suas meias-vidas? (c) Quantos núcleos de cada tipo estão inicialmente presentes na amostra? (d) Quantos núcleos de cada tipo estão presentes para ?
Passo 1
(a) Bom pessoal, a gente sabe que a equação que governa esse fenômeno de decaimento é essa aqui:
Onde a constante de decaimento se relaciona com a meia vida por essa equação:
Beleza. Então olha o que acontece com aquele equação lá de cima quando a gente aplica o logaritmo dos dois lados:
E lembrando que , então:
Mas como :
Beleza, então a gente pode linearizar a equação pra encontrar uma função que é:
Que tem que ser uma reta! Já que a equação é do tipo:
Onde o nosso coeficiente linear vai ser a constante de decaimento .
Então vamos fazer essa tabela (vamos precisar de uma calculadora!):
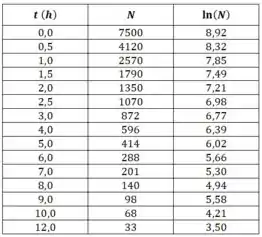
Passo 2
Beleza, agora é hora de pegar um papel milimetrado (ou um computador!) e fazer esse gráfico.
Vamos colocar esses pontos. No eixo vamos colocar os valores da primeira coluna, e no eixo vamos colocar os valores da terceira coluna.
O gráfico tem que ficar mais ou menos assim:
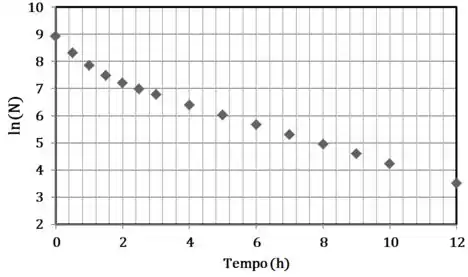
Poxa, mas não deveria ser uma linha reta? É aí que entra a nossa tarefa. Pode ser que tenha mais de um elemento sendo registrado aí!
Se você olhar bem para o seu gráfico, vai ver que dá pra separar dois trechos aí em que a curva é muito próxima de uma reta:
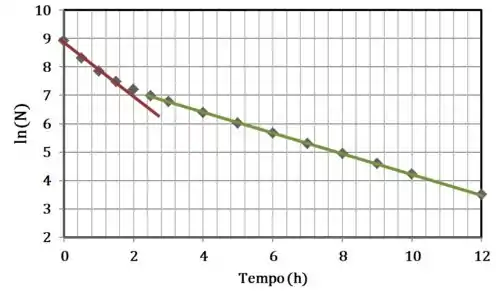
Ok, então vamos dizer que temos duas espécies diferentes.
Passo 3
(b) Ok, então vamos calcular os coeficientes lineares em cada um desses trechos, que são as nossas constantes de decaimento.
Olhando para a reta verde primeiro, escolha dois tempos quaisquer, podem ser os da tabela mesmo!
E então o coeficiente angular é:
E como :
E então a meia-vida é:
E se você prolongar a reta verde, vai ver que ela toca o eixo bem perto do (não precisa ser muito preciso aqui!). Isso quer dizer que:
Então podemos completar a nossa fórmula:
Passo 4
Agora a gente quer fazer a mesma coisa para a linha vermelha.
Vamos pegar os pontos que tem a abcissa entre e mais ou menos . Olhando a tabela:
Mas vamos tentar remover o efeito da segunda amostra (da linha verde). Pra isso vamos ver quantas contagens a segunda amostra gera nesses dois pontos:
Então, subtraindo:
E tirando os logaritmos:
E nesse caso o coeficiente angular é:
E então a constante de decaimento seria:
E a meia vida:
E como a gente já viu que o número de decaimentos seria em , então já dá pra construir nossa equação:
Passo 5
(c) Tá, agora vem um problema. Quantas amostras estão presentes inicialmente na amostra?
Bom pessoal, uma forma de resolver isso é integrando as equações que a gente achou.
Já que dá o número de decaimentos por segundo em uma determinada hora, se a gente multiplicar por :
Vamos ter uma função aproximada para o número de decaimentos por segundo. Agora é só integrar isso com indo de até .
Começando com a amostra da reta verde:
E para a reta vermelha:
Passo 6
(d) Agora queremos saber quandos núcleos de cada tipo ainda estão presentes quando .
É só usar as nossas integrais de novo! Mas dessa vez vamos integrar só a partir de !
Por que isso? Porque assim estamos pegando todos núcleos que ainda estavam “vivos” em , e só desapareceram nesse intervalo :
A primeira integral fica:
E a segunda:
Pronto! Calculamos tudo que foi pedido!
Uma coisa é importante destacar aqui. Nós usamos um método bem simplficado pra calcular os coeficientes das nossas retas lá em cima!
A vantagem desse método é que dá pra fazer sem usar o computador. Só não estranhe se você fizer no computador, com um método mais sofisticado, e achar uma resposta um pouquinho diferente! Mas a nossa resposta já é uma aproximação muito boa!
Resposta
(a) Temos dois nucleotídeos diferentes.
(b) As meias vidas são e .
(c) Inicialmente temos núcleos do tipo que tem meia vida mais longa, e núcleos do tipo com vida mais curta.
(d) Em , o número de núcleos do tipo com vida longa é , e do tipo com vida curta é .