Uma partícula de masa está suspensa do teto por uma mola de constante elática e comprimento relaxado , cuja massa é desprezível. A partícula é solta em repouso, com a mola relaxada. Tomando o eixo orientado verticamente para baixo, com origem no teto, calcule a posição da partícula em função do tempo.
Passo 1
Vamos começar fazendo um desenho do instante inicial, com a mola relaxada e a origem no teto:
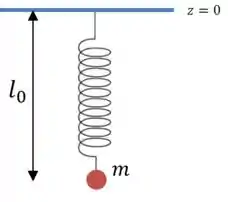
Como estamos na vertical, temos duas forças agindo sobre a mola: a força peso, e a força elástica.
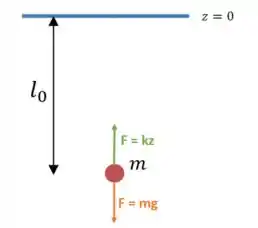
Vamos escrever isso usando a segunda lei de Newton:
O sinal negativo aparece por conta da lei de Hooke ().
Passo 2
Como a aceleração é a segunda derivada da posição que no caso é representada pela coordenada :
Temos a seguinte equação diferencial:
Substituindo a aceleração:
Dividindo todos os lados pelo valor da massa da partícula:
Essa é uma EDO não homogênea (porque temos aquela constante sozinha do lado direito da equação).
O método pra resolver esse tipo de equação é: primeiro resolva como se a constante não estivesse lá. Depois coloque a constante de volta e tente chutar uma solução que funcione.
A solução geral é a soma dessas duas soluções!
Passo 3
Então vamos começar com a solução da equação homogênea, ou seja, vamos começar fingindo que não está ali:
Nesse caso temos a equação geral de um oscilador harmônico, que tem a seguinte solução:
Onde :
Passo 4
Agora vamos para a solução não homogênea:
Podemos chutar uma solução constante, ou seja,
Nesse caso teríamos que a segunda derivada é igual a zero:
Então:
Então nossa segunda solução é:
Agora temos que juntar as duas:
Passo 5
Beleza, achamos a solução geral, agora temos que impor as condições iniciais.
O enunciado diz que a partícula é solta em repouso, isso quer dizer que a velocidade inicial é igual a zero, e como sabemos que a velocidade é igual a primeira derivada da posição em relação ao tempo:
Logo:
Ou seja, a velocidade inicial é zero. Vamos derivar a nossa função :
E quando , temos:
Para satisfazer essa equação, vamos definir que , já que .
Então por enquanto temos o seguinte:
Passo 6
Outra informação que temos é que a partícula parte da posição , ou seja:
Substituindo na nossa função, ficamos com:
Como o cosseno de 0 é igual a 1:
Então:
Resposta
A posição da partícula em função do tempo é
.