Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 43
Por meio de uma força horizontal e constante de , Doug empurra um caixote de sobre uma rampa com de inclinação e sem atrito até subir verticais. Quanto vale a velocidade do caixote no topo da rampa?
a. Resolva este problema usando trabalho e energia.
b. Resolva o problema usando as leis de Newton.
Passo 1
Vamos desenhar o que está sendo dito no enunciado se atentando que o caixote sobe uma rampa
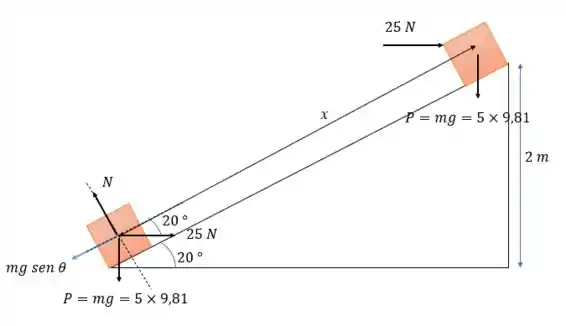
Fazendo por trabalho e energia nós temos que a variação da energia cinética vale o trabalho total e que vale:
O trabalho total é nada mais que o trabalho de todas as forças que atuam na caixa, com sendo o trabalho da normal, o trabalho da força gravitacional e o trabalho que o Doug faz ao empurrar a caixa na horizontal. E como trabalho atua na direção do deslocamento então:
Pois a força normal está na perpendicular com a rampa.
Com sendo (pela propriedade trigonométrica de um triângulo retângulo)
Então:
E o trabalho da força gravitacional é o trabalho de (apontada no desenho) na direção contra o movimento, ou seja:
Considerando a velocidade inicial como nula nós teremos então a velocidade final do bloco sendo de:
Passo 2
Agora pelas leis de Newton, nós devemos considerar que a força de e a força peso do bloco (projetada no eixo do plano) geram uma força resultante tal que:
De forma que a aceleração que esse corpo sofre será de:
E como o corpo está sendo acelerado então por Torricelli:
Com
Logo:
Mesmo resultado que no passo anterior.