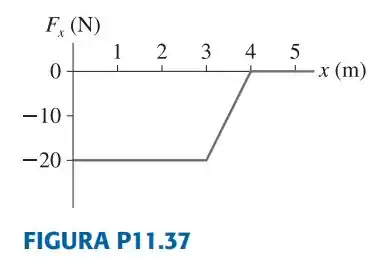
Uma partícula de experimenta a força conservativa e unidimensional representada na FIGURA P11.37.
a. Desenhe um gráfico que represente a energia potencial desde até . Considere nula a energia potencial em .
Sugestão: pense a respeito da definição de energia potencial e da interpretação geométrica do trabalho realizado por uma força variável.
b. A partícula é disparada para a direita a , a partir de . Qual é a energia mecânica da partícula?
c. Desenhe a linha da energia total no gráfico desenhado no item .
d. Onde se encontra o ponto de retorno da partícula?
Passo 1
Sabendo que a força é conservativa então temos que a variação da energia potencial será dada por:
Então vamos montar o gráfico junto. De até temos uma força constante de , logo o trabalho realizado pela partícula de até será:
Então:
Onde a curva de comportamento dessa energia potencial segue uma reta .
Ou seja:
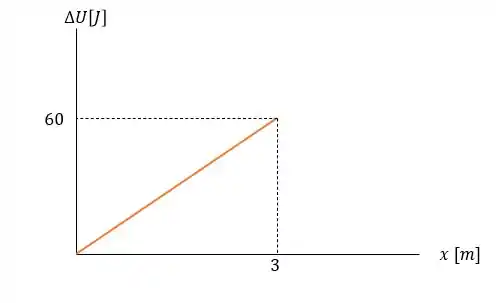
Uma coisa que temos que ver é que:
Passo 2
Agora no intervalo de até a força varia de modo a ter uma reta crescente. Portanto a variação da energia potencial será a de uma parábola com concavidade apontada para baixo de forma que teremos uma variação de energia potencial igual a área positiva do triângulo entre a força e o eixo horizontal igual a:
Então o gráfico ficará igual a:
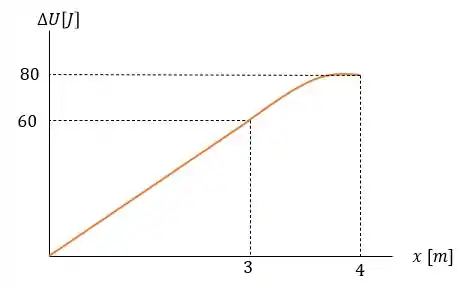
E como não há mais força em , portanto não há mais nenhuma adição de energia no sistema, deixando o gráfico como:
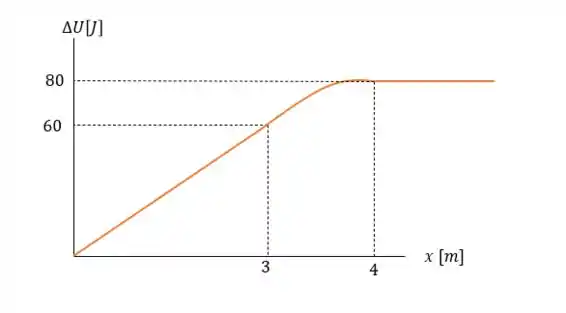
Passo 3
Para a letra nós devemos saber que a energia mecânica de uma partícula (para um sistema simples sem perdas, é dada por):
Onde é a energia cinética e a potencial.
E para a energia está na reta de , portanto a energia mecânica será de:
E como é conservativo então é um valor constante. E que será visto na figura abaixo:
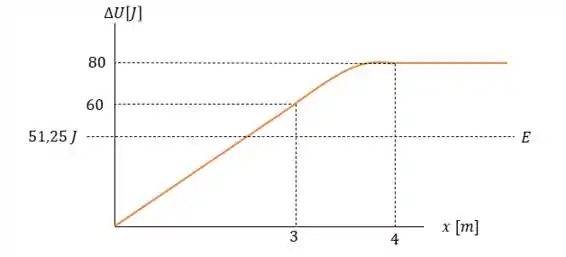
E essa imagem responde a letra .
Passo 4
Ponto de retorno é onde a energia potencial e a energia mecânica se igualam, pois aí temos e quando Quando a velocidade dessa partícula é nula (imaginando uma massa-mola esticando e comprimindo, é quando a massa volta ao estado em que foi largada , considerando que ela partiu do repouso).
Então vendo a linha que a energia mecânica corta o gráfico da energia potencial vemos que ela corta o gráfico na reta , portanto:
Essa é a posição de retorno da partícula.