Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.Problemas - Ex. 75

Uma mola cuja constante é igual a 40,0   N / m e comprimento de 0,60   m , está presa a um bloco de 0,500   k g apoiado em repouso sobre uma mesa de ar horizontal sem atrito, sendo A a posição inicial do ponto de contato entre o bloco e a mola (Figura 7.44). A massa da mola é desprezível. Você move o bloco para a direita ao longo da superfície puxando-o com uma força horizontal constante de 20,0   N . a) Qual é a velocidade do bloco quando sua parte traseira atinge o ponto B, situado a 0,25   m à direita do ponto A? b) Quando a parte traseira do bloco atinge o ponto B, você liberta o bloco. No movimento posterior, qual é a distância mínima entre o bloco e a parede onde a mola está presa?

Passo 1

Olá, meu querido amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Temos uma situação onde uma força constante desloca um corpo preso em uma mola, fazendo o mesmo se movimentar sobre a ação de resistência da mola, que quer fazer o mesmo voltar a posição de equilíbrio.

A força F faz o corpo se movimentar, e queremos saber qual será a velocidade que ele chegará no ponto B, sobre a ação destas duas forças.

Passo 2

  1. Oi, galerinha! Tudo bom? Para resolver essa questão vamos aplicar a conservação da energia! Temos que para o momento A e B

    2. W o u t r a = K A + U A = K B + U B

    K energia cinética

    U energia potencial

    Como o bloco está em repouso no momento A, temos que

    K A = 0

    Já para o momento B

    K B = 1 2 m v B 2

    A energia potencial elástica em A também será zero,

    U A = 0

    U B = U B , e l = 1 2 k x B 2

    onde x B = 0,25 m

    Logo,

    W o u t r o = W F = F x B

    Então,

    F x B = 1 2 m v B 2 + 1 2 k x B 2

    Passo 3

    O trabalho realizado por F vai em parte à energia potencial da mola esticada e em parte à energia cinética do bloco.

    Assim,

    F x B = 20 N ⋅ 0,25 m = 5 J

    E

    1 2 k x B 2 = 1 2 40 N ⋅ 0,15 m 2 = 1,25 J

    Então,

    5 J = 1 2 m v B 2 + 1,25 J

    Isso implica que:

    v B = 2 ⋅ 3,75 J 0,500 k g = 3,87 m / s

    Passo 4

  2. Vamos aplicar a equação ∆ K + ∆ U + ∆ U i n t = 0 ao movimento do bloco.

Seja o ponto C onde o bloco está mais próximo da parede. Quando o bloco está no ponto C, a mola é comprimida uma quantidade x C , para que o bloco esteja a 0,60 m - x C da parede, e a distância entre B e C é x B + x C .

Vamos descrever o movimento de A para B para C:

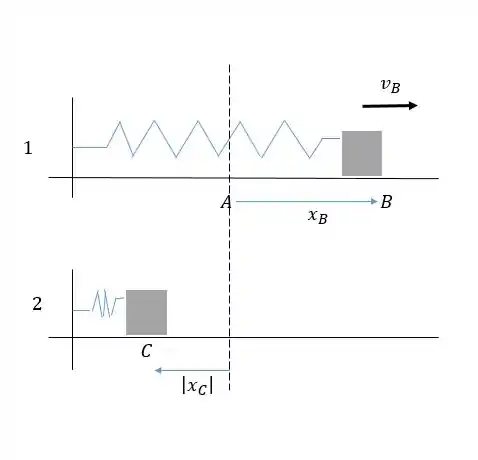
Temos que:

K B + U B + W o u t r a = K C + U C  

Uma vez que:

W o u t r a = 0

Passo 3

Do item a) podemos tirar que:

K B = 1 2 m v B 2 = 5 J - 1,25 J = 3,75 J

Como,

U B = 1 2 k x B 2 = 1,25 J

K C = 0

instantaneamente em repouso no ponto mais próximo da parede e

U C = 1 2 k x C 2

Então,

3,75 J + 1,25 J = 1 2 k x C 2

Isso implica que:

x C = 2 ⋅ 5 J 40 N / m = 0,50 m

A distância do bloco da parede é de 0,60   m - 0,50   m = 0,10   m .

Resposta

  1. v B = 3,87 m / s
  2. A distância do bloco da parede é de 0,10   m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força paralela ao eixo Ox atua sobre uma partícula que se desloca ao longo deste eixo. Essa força produz uma energia potencial dada por U x = α x 4 , onde α = 1,20J / m 4 . Qual é aforça (módulo,
A energia potencial entre dois átomos de hidrogênio separados por uma distância x muito grande é dada por U x = - C 6 / x 6 , onde C 6 é uma constante positiva. Qual é a força que um átomo exerce sobr
Duas massas, m 1 e m 2 , estão sobre o eixo xy, estando m 1 posicionado no lugar de origem e m 2 , na posição x e livre para mover-se por uma distância r de um ponto P com coordenadas x e y (Figura 7.
Em um acidente, um carro atropelou um pedestre, e em seguida o motorista pisou nos freios para parar o carro. Durante o julgamento, o advogado do motorista alegou que ele obedecia ao limite de velocid
Uma haste de madeira de massa desprezível e comprimento igual a 80,0c m é pivotada em torno de um eixo horizontal que passa através de seu centro. Um rato branco com massa de 0,500k g fica agarrado a