Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 11.3 - Ex. 6
Duas pessoas transportam uma prancha de madeira uniforme com 3,0 m de comprimento e peso de 160 N. Se uma das pessoas aplica em uma extremidade uma força de baixo para cima
de 60 N, em qual ponto a outra pessoa deve suspender a prancha? Comece com um diagrama do corpo livre para a prancha.
Passo 1
Vamos esboçar o diagrama do corpo livre da placa:
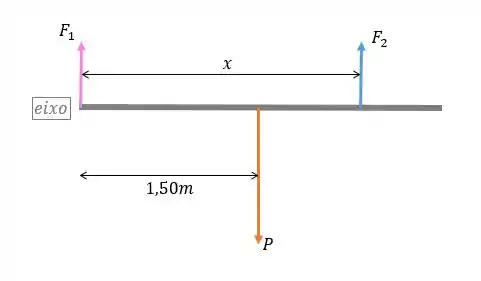
Como a prancha é uniforme, seu centro de a gravidade é de 1,50 m de cada extremidade.
Vamos aplicar as condições de equilíbrio:
com para cima.
com o eixo no final onde a primeira pessoa aplica uma força e com torques no sentido anti-horário positivos.
Passo 2
Fazendo:
Temos que:
Passo 3
E fazendo:
Temos que:
A outra pessoa levanta com uma força de em um ponto a do final onde a outra pessoa levanta.
Resposta
A outra pessoa levanta com uma força de em um ponto a do final onde a outra pessoa levanta.