Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 46
Uma mola horizontal de constante elástica é comprimida em e usada para lançar uma caixa de sobre uma superfície horizontal e livre de atrito. Após a caixa ter percorrido certa distância, a superfície torna-se áspera. O coeficiente de atrito cinético da mesma passa a ser de . Use trabalho e energia para determinar que distância a caixa escorregará sobre a superfície áspera até parar.
Passo 1
Vamos desenhar essa caixa nas diversas situações descritas na questão:
Essa primeira imagem é da condição inicial do bloco e da mola.
E aqui podemos escrever que a energia mecânica desse sistema é igual a energia elástica da mola, ou seja:
Passo 2
E após o objeto ter deslocado uma certa distância após ser liberado da mola o objeto entra numa região áspera (e com uma certa velocidade também) e podemos ver ela abaixo.
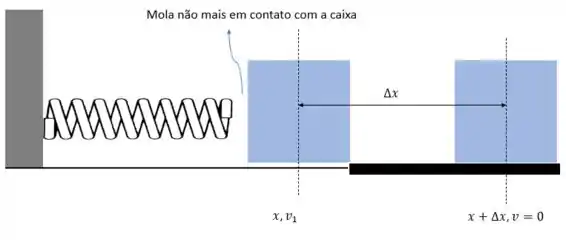
Quando a caixa se desgruda da mola toda a energia potencial elástica é transferida em energia cinética para caixa (pois a energia mecânica passa a ser inteiramente a cinética) e essa energia se mantém até a caixa entrar na região áspera e perder energia com o atrito.
Então pelo teorema energia cinética- trabalho temos:
A que diminuirá a energia cinética do bloco é igual a força de atrito e que vale
Então:
A normal do bloco é a mesma que a força peso, pois o piso é plano, então:
Portanto o bloco desliza no plano áspero até parar.