Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 50
Use trabalho e energia para determinar o valor de velocidade do bloco de da FIGURA P11.50 imediatamente antes de bater no solo
(a) se a mesa for desprovida de atrito e
(b) se o coeficiente de atrito cinético do bloco de for de .
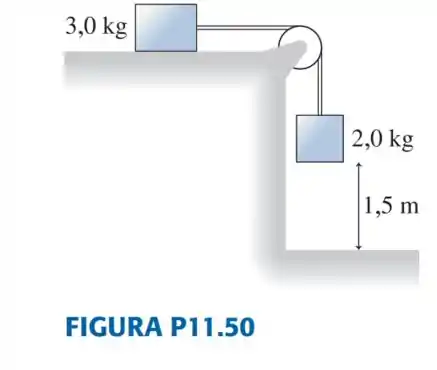
Passo 1
Vamos modelar esse sistema para a situação antes de começar a se movimentar e quando o bloco de cai no chão.
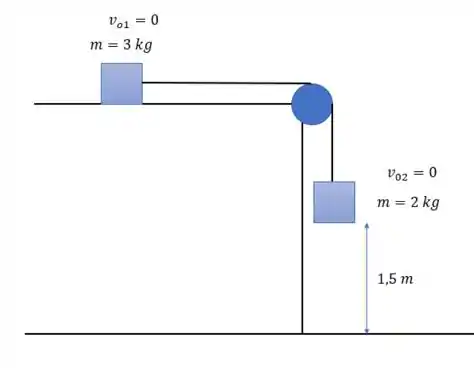
E aqui podemos dizer que a força de tração não interfere na equação de energia pois pensa só, a força de tração atua a favor do movimento do bloco de massa de mas é contra o movimento do bloco de , e como eles se movimentam na mesma distância então o trabalho de um anula com o do outro.
Então vamos modelar nossa equação de energia, no começo não temos energia cinética, só temos a energia potencial gravitacional da massa de de modo que:
E o modelo de energia no instante que o bloco de toca no chão é tal que somete temos a energia cinética, ou seja:
Só que para blocos que estão conectados por um fio nós temos que os dois blocos estão sob a mesma aceleração, logo:
E pela conservação da energia então:
Passo 2
Considerando agora um atrito entre a mesa e o bloco de nós teremos a diferença:
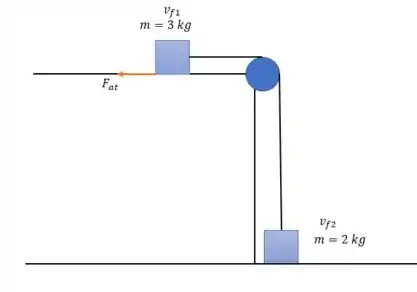
Isso muda nosso modelo de energia de forma a termos:
Pois o bloco movimenta-se que é a mesma altura de queda do bloco de , e os blocos continuam tendo a mesma aceleração durante todo o processo.
E devemos encontrar uma menor velocidade pra o caso com atrito do que sem atrito, afinal o atrito é uma perda de energia.