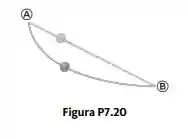
Como mostrado na Figura P7.20, uma conta clara de massa 25 g desliza por um fio reto. O comprimento do fio do ponto A ao ponto B é 0,600 m, e o ponto A é 0,200 m mais alto que o ponto B. Uma força de atrito constante de módulo 0,025 N atua sobre a conta. (a) Se a conta é liberada do repouso no ponto A, qual é a sua velocidade no ponto B? (b) Uma conta escura de massa 25 g desliza ao longo de um fio curvo, sujeita a uma força de atrito com o mesmo módulo constante da conta clara. Se ambas as contas são soltas simultaneamente do repouso no ponto A, qual delas chega ao ponto B com maior velocidade? Explique.

(a)Pela conservação de energia, a energia potencial gravitacional que a conta tinha no ponto A, mais alto em , vai virar totalmente energia cinética no ponto B. Só que ao longo do percurso, uma parte da energia é perdida por atrito.

Matematicamente, a gente tem isso:

Aplicando as formulinhas, temos:

Aplicando os dados que a gente tem, cuidando das unidades, e considerando ficamos com: