Enunciado
Física - Young and Freedman - Vol 1- Ed: 10º - Capítulo 7.Problemas - Ex. 68
Um objeto possui diversas forças atuando sobre ele. Uma das forças é dada por uma força orientada no sentido positivo do eixo Ox cujo módulo depende da posição do objeto. O valor da constante é dado por. O objeto se move ao longo da seguinte trajetória:
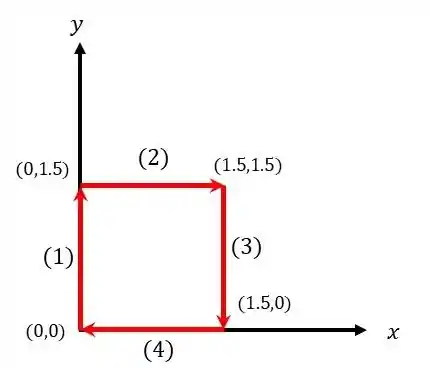
(1) ele parte da origem e se move ao longo do eixo Oy ao ponto x=0, y=1.5m
(2) move-se paralelamente ao eixo Ox ao ponto x=1.5m, y=1.5m
(3) move-se paralelamente ao eixo Oy ao ponto x=1.5m, y=0
(4) move-se paralelamente ao eixo Ox retornando para a origem.
a) Faça um esboço dessa trajetória no plano xy.
b) Calcule o trabalho realizado pela força em cada etapa da trajetória e o trabalho total realizado no percurso fechado.
c) A força é conservativa ou não conservativa? Explique.
Passo 1
Beleza pessoal?! Espero que esteja tudo bem com meu os herdeiros de Newton. Vamos dar início a mais uma resolução com o padrão de qualidade do Responde aí, então pegue seu lápis, caderno e café e vamos nessa!!!
Sabemos que o trabalho realizado por uma força variável F⃗ em uma partícula movendo-se ao longo de um caminho de P1 para P2 é dado por:
Onde dl⃗ é o deslocamento infinitesimal.
- Primeiro, reescrevemos a função força depois de substituir o valor de αα, então temos:
Passo 2
(1) Para o caminho de P⃗1=(0,0) a P⃗2=(0,1.5)
Como a partícula está se movendo em uma trajetória paralela ao eixo y, então o deslocamento infinitesimal é dado por:
Para o caminho de P⃗1=(0,1.5) a P⃗2=(1.5,1.5):
Como a partícula está se movendo em uma trajetória paralela ao eixo xx, então o deslocamento infinitesimal é dado por:
Como y é constante e tem valor igual a 1,5 obtemos:
(3) Para o caminho de P⃗1=(1.5,1.5) a P⃗2=(1.5,0):
Como a partícula está se movendo em uma trajetória paralela ao eixo yy, então o deslocamento infinitesimal é dado por:
Passo 2
(4) Para o caminho de P⃗1=(1.5,0) a P⃗2=(0,0):
Como a partícula está se movendo em uma trajetória paralela ao eixo xx, então o deslocamento infinitesimal é dado por:
Como y é constante e tem valor igual a 0, obtemos:
Portanto, o trabalho total realizado nesta rodada completa é:
(c) Como o trabalho total realizado em uma viagem de ida e volta completa não é zero zero, então a força F⃗ é uma força não conservativa não conservativa.
Resposta
Ver o desenvolvimento