Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.5 - Ex. 38
O nível da água no interior em um tubo de vidro vertical com de comprimento pode ser ajustado para qualquer posição. Um diapasão vibrando a é mantido acima da extremidade aberta do tubo para gerar uma onda sonora estacionária na parte superior do tubo, onde existe ar. (Essa parte superior cheia de ar se comporta como um tubo com uma extremidade aberta e a outra fechada).
a) Para quantas posições diferentes do nível de água o som do diapasão produz uma ressonância na parte do tubo cheia de ar? Qual é (b) a menor altura e (c) qual é a segunda menor altura da água no tubo para as quais ocorre ressonância?
Passo 1
Opa, tudo certinho aí?
Então, vamos lá! O que essa questão tá falando é da ressonância do som do diapasão com a onda sonora no tubo. Mas o que essa ressonância significa mesmo? Significa que as frequências das duas ondas são iguais! Isso já dá uma informação pra gente
Passo 2
Já temos também uma segunda informação: o som está se propagando no ar, e como toda boa onda sonora que se propaga no ar a sua velocidade é
Com isso já podemos calcular o comprimento de onda!
Show! Já temos as informações da onda dentro do tubo :D
Passo 3
Agora vamos olhar o enunciado de novo: lá a gente tem um tubo de de comprimento cheio de água. Se a altura da coluna de água é vamos ter um tubo com uma extremidade aberta de comprimento , como a figura a seguir
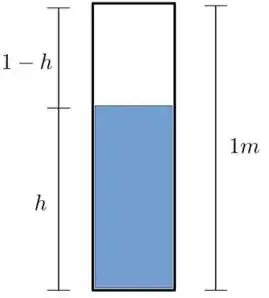
Bem, vamos lá! Agora temos que analisar os modos normais. Já temos o comprimento de onda de cada modo normal, só falta saber quais modos normais são possíveis.
Lá da teoria a gente viu que os modos normais de um tubo com uma extremidade aberta e outra fechada têm um nó na extremidade fechada e um ventre na extremidade aberta.
No primeiro modo normal dentro do comprimento do tubo temos de comprimento de onda, ou seja:
No próximo modo normal dentro do comprimento do tubo temos comprimento de onda
No terceiro modo normal dentro do comprimento do tubo temos comprimento de onda
No quarto modo normal dentro do comprimento do tubo temos comprimento de onda
Agora vamos ver o quinto modo, onde no tubo temos comprimentos de onda
Opa! Não tem como ter uma altura negativa da coluna de água não é mesmo?! Isso significa que não tem como ter o quinto modo! Só podemos ter do primeiro até o quarto modo, ou seja, só temos 4 modos possíveis com esse comprimento de onda, beleza?
Essa é a reposta do item (a)! Temos 4 posições diferentes que tem ressonância com o diapasão ;)
Passo 4
Aí é bem rápido olhar as letras (b) e (c), não é mesmo? A menor altura é e a segunda menor é .
Show! Partiu pra próxima!
Resposta
- 4 Posições
- 0,125 m
- 0,375 m